Medidas de intensidad sísmica independientes de la orientación del sensor: Aplicación a una base de datos con acelerogramas de Costa Rica, El Salvador y Nicaragua
Luis A. Pinzón, M.Sc.
Universidad Tecnológica de Panamá
[email protected]
Diego A. Hidalgo, M.Sc.
Universidad de Costa Rica
[email protected]
Lluís G. Pujades, Ph.D.
Universidad Politécnica de Cataluña
[email protected]
Resumen— En esta investigación se han comparado las medidas de intensidad del movimiento del suelo, para una base de datos con acelerogramas de Costa Rica, Nicaragua y El Salvador. Estas medidas están basadas en una serie de registros de aceleración ortogonales horizontales, rotados para todos los ángulos no redundantes, de tal manera que se proponen medidas que son independientes de la orientación de los sensores.
Estas medidas son: GMRotDpp y GMRotIpp, donde “pp” representa el percentil, comúnmente “50” y las letras D e I, indican dependencia o independencia del periodo de la estructura. Para determinar GMRotDpp, se define para cada oscilador, el ángulo correspondiente del percentil deseado (pp), esto ordenando de manera creciente los valores obtenidos para cada rotación, no pudiendo definir un solo ángulo válido para todos los períodos, por lo cual se dice que es dependiente del período. Por su parte GMRotIpp, requiere del cálculo previo de GMRotDpp, y define un único ángulo para el cual la medida se aproxima con el menor error posible al valor dependiente del período, siendo esta medida independiente del período.
Estas dos medidas fueron comparadas entre sí, encontrando una relación que permite determinar qué medida es la más adecuada para cada caso de estudio. Al mismo tiempo fueron comparadas con la máxima respuesta espectral esperada definida por la media cuadrática y se obtuvieron relaciones que fueron comparadas con otras obtenidas en diferentes investigaciones.
Un resultado relevante de esta investigación ha sido el análisis del efecto de direccionalidad, entendido como la dependencia de la media geométrica de la respuesta espectral de las componentes horizontales con el ángulo de orientación del instrumento de registro, y la obtención de nuevas medidas independientes del ángulo.
Palabras Claves— Acelerogramas, Análisis Espectral, Dinámica, Direccionalidad, Espectro de Respuesta, Sísmica, Sismo, Sismología.
Abstract— This research compares the measures of ground motion intensity, for an accelerograms’ database from Costa Rica, Nicaragua and El Salvador. These measures are based on a series of orthogonal- horizontal acceleration records, rotated for all non-redundant angles, so we proposed measures that are independent of the orientation of the sensors.
These new measures are: GMRotDpp and GMRotIpp, where "pp" represents the percentile, commonly "50", and D or I represent the dependence or independence of the period. For the calculation of GMRotDpp, it is necessary to define the angle of rotation required to obtain the value of the percentile (pp), arranging in an increasing way the values obtained for every rotation, not being able to define a single angle that´s valid for the measure, thus establishing the dependence of the period.
On the other hand, GMRotIpp, requires the calculation of GMRotDpp, and defines a single angle, to which the measure approximates, with the least error possible, to the dependent value of the period, being this measure independent of the period.
These two measures were compared in order to find a relationship between them and to determine what action is most appropriate for each case of study. At the same time, the measures were compared with the maximum expected spectral response (RMS) defined by the quadratic mean, obtaining the relations that were also compared with some results from different authors.
An important result of this research is the analysis of the directionality effect, understood as the dependence of the geometric mean from the horizontal components with orientation angle of the recording device, and obtaining new measurements independent of the angle.
Keywords— Accelerogram, Directionality, Dynamic, Earthquake, Response Spectrum, Spectral Analysis, Seismic, Seismology.
Tipo de artículo: Original
Fecha de recepción: 12 de marzo de 2015
Fecha de aceptación: 12 de mayo de 2015
1. Introducción
Gran parte de las ecuaciones para predecir el movimiento del suelo debido a sismos (leyes de atenuación con la distancia), emplean la respuesta espectral correspondiente al movimiento horizontal como parámetro de intensidad [1]. Usualmente, los registros de aceleraciones horizontales son obtenidos de componentes orientadas ortogonalmente, por lo que hay dos registros disponibles para cada evento.
Hay muchas maneras de combinar la respuesta de las componentes horizontales en las ecuaciones de predicción de movimientos del terreno [2], entre las cuales se puede mencionar: la media aritmética (AM), la media geométrica (GM), la media cuadrática (QM) o el máximo valor de cada componente. En la derivación de algunas ecuaciones de predicción del movimiento del suelo, como las propuestas por Boore et al. [3], estas dos componentes se combinan en una única medida de intensidad del movimiento, para formar la media geométrica del espectro de respuesta para cada componente horizontal [4].
Una ventaja de la GM es que la variabilidad de los resultados obtenidos en las regresiones empleadas para las ecuaciones de predicción del movimiento del suelo, es menor con respecto a otras medidas comúnmente empleadas [1], sin embargo, la GM de la respuesta estructural tiene un inconveniente potencialmente importante: no es invariante a la orientación de los sensores.
Como un caso extremo, consideremos las señales libres de ruido, linealmente polarizado. Si uno de los sensores resulta estar alineado con la dirección de polarización, el espectro de respuesta del movimiento registrado en el sensor ortogonal sería cero, independientemente de la amplitud de la polarización del movimiento del suelo. Ésta es una consideración importante para registros de sismos cercanos al origen, donde la orientación de la ruptura y el patrón de radiación, incluyendo los efectos de directividad, pueden producir fuertes movimientos correlacionados en particular en los períodos de 1 segundo o más [5].
Debido a que obtener el espectro de respuestas no es una operación lineal en una serie de tiempo (el espectro de respuesta de la suma de dos series de tiempo, no es igual a la suma del espectro de respuesta para cada serie de tiempo), la sensibilidad a la orientación del sensor también es compartida por muchas otras medidas de intensidad de movimiento de suelo.
En este trabajo se utilizan dos medidas de intensidad del movimiento del suelo que son independientes de la orientación de los instrumentos de registro [6]. Estas dos medidas se obtienen al computar la media geométrica del espectro de respuesta para todas las rotaciones no redundantes, de las componentes horizontales de un registro de aceleraciones.
Las medidas determinadas son la GMRotDpp y GMRotIpp, donde “pp” representa el percentil, comúnmente 50 y las letras D e I indican que es dependiente o independiente del período de la estructura. Al utilizar estas medidas, se elimina la orientación del sensor como un componente de la incertidumbre aleatoria, lo cual puede ser importante en cálculos probabilistas de riesgo sísmico de movimientos de suelo con una frecuencia anual de excedencia baja [7].
2. Base de datos
La base de datos disponible, posee registros de Costa Rica, El Salvador y Nicaragua, registrados en el período comprendido entre 1967 y 2012. Entre estos tres países se tiene un total de 1010 sismos, que se traduce en 3191 registros de aceleraciones, todos con dos componentes horizontales y una vertical. De este total, hay 1328 acelerogramas registrados en Costa Rica, 262 sismos registrados en Nicaragua y 1601 en El Salvador. Los registros fueron recopilados por el Ing. Víctor Schmidt en su trabajo final de doctorado [8] y el Laboratorio de Ingeniería Sísmica de la Universidad de Costa Rica [9].
Vale la pena observar que esta base de datos fue usada por Schmidt [8] y Schmidt et al. [10] para la obtención de leyes predictivas del movimiento del suelo (leyes de atenuación) en Costa Rica; la mayoría de los acelerogramas corresponden a registros en campo abierto (en superficie y/o en roca) y, aunque algunos fueron registrados en la base (nivel más inferior) de edificios, su contenido frecuencial representa bien el registro en campo libre ya que no está alterado de forma significativa por la respuesta estructural.
De estos registros, se seleccionaron aquellos con una aceleración máxima de cualquiera de sus dos componentes horizontales, superior o igual a 10 gal (10 cm/s2), resultando 1406 registros, cada uno con sus tres componentes ortogonales. Tanto el tratamiento estadístico de la base de datos como la selección de acelerogramas y su tratamiento preliminar, se realizaron mediante programas en MATLAB, desarrollados por los autores de este estudio.
El objetivo de este trabajo es estudiar el efecto de direccionalidad para una extensa base de datos de Centroamérica y comparar los resultados con los obtenidos por otros autores. En estos estudios previos, véase por ejemplo Boore et al. [6], no se consideran aspectos como la cercanía o no a fallas, el tipodesuelo, laduraciónoelcontenidofrecuencial, y en consecuencia, aun reconociendo su importancia, no se han considerado tampoco aquí. La influencia de la direccionalidad en la incertidumbre aleatoria de las leyes predictivas parece ser poco significativa [1] aunque probablemente, como indica Boore et al. [6], los efectos de direccionalidad pueden ser más relevantes cuando las dos componentes horizontales están fuertemente correlacionadas como pueden ser movimientos impulsivos cerca de las fallas así como en casos relacionados con fenómenos de directividad y efectos de movimientos perpendiculares o paralelos a la falla.
3. Metodología
La metodología utilizada se basa en la propuesta de Boore et al. [6]. Esta metodología se ha adaptado a las características de los datos disponibles y se ha complementado con una serie de procedimientos orientados a caracterizar la base de datos disponible y al cálculo de los espectros.
3.1 Media Geométrica de Espectros de Respuesta
Debido a la dependencia que posee la media geométrica de la respuesta espectral al ángulo de rotación, Boore et al. [6] definen dos medidas del movimiento del suelo, correspondientes a un cierto percentil del conjunto de medias geométricas obtenidas utilizando todas las rotaciones no redundantes.
Se utilizan combinaciones lineales de las componentes rectangulares entre 0 y 90 grados de rotación, debido a que las combinaciones lineales de la señal, poseen una periodicidad en este intervalo. Este hecho se puede apreciar cuando se calcula el valor de la aceleración pico del terreno (PGA por sus siglas en inglés), el cual toma valores simétricos a partir de los 90 grados. La GM, al ser una combinación de las dos direcciones ortogonales, posee el mismo valor pues no depende del orden de los factores que la componen.
A pesar de que la definición de GMRotDpp satisface el requisito de ser independiente de la orientación del sensor, tiene la deficiencia de que una única rotación no produce dos series de tiempo para las cuales la media geométrica del espectro de respuesta individual sea igual a GMRotDpp para todos los períodos considerados.
Por ese motivo, se calcula una medida que sea independiente de la orientación del sensor y del período, denominada GMRotIpp. Con esta medida se pretende obtener un único espectro de respuesta, que será independiente del ángulo del registro y del período de la estructura. Vale la pena observar que este espectro GMRotIpp es útil tanto para el análisis espectral como para el análisis dinámico de estructuras, ya que permite definir también la serie temporal que lo genera.
3.1.1 GMRotDpp
Para calcular GMRotDpp se generó un programa en MATLAB y se siguieron los pasos descritos por Boore et al. [6], que se resumen a continuación.
a) Todos los cálculos se realizan a partir de los archivos resultantes del proceso de filtrado, donde para uniformizar el cálculo y post-procesamiento de los espectros de respuesta, se aplica un filtro pasa banda acasual tipo Butterworth de orden 3, con una frecuencia máxima de 20 Hz y para el caso de las frecuencias bajas se utiliza un valor de 0.10Hz. A cada una de las componentes de aceleraciones se les nombró como acc_f_n(t,n,ϴ) (N-S) y acc_f_e(t,n,ϴ) (E-O), donde t es el tiempo del registro, n es el porcentaje del amortiguamiento crítico del oscilador y ϴ indica la rotación del ángulo respecto a las condiciones iniciales.
b) Se estableció el ángulo de rotación ϴ a 0.0, como ángulo de partida.
c) Se forma la serie de tiempo para el ángulo de rotación ϴ, utilizando combinaciones lineales de las series de tiempo definidas en el paso a). Las ecuaciones que definen estas combinaciones lineales son:
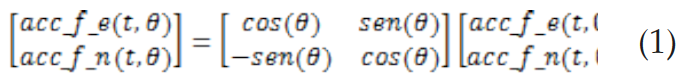
Donde por simplicidad se elimina “n”, pues en todos los casos se emplea el mismo factor de amortiguamiento crítico del 5 %.
d) Se calcularon los espectros de respuestas correspondientes a cada ángulo de rotación. Así, para todos los ángulos de rotación tendremos un espectro de respuesta para ambas componentes horizontales ER1(ϴ,T) y ER2(ϴT) .
e) Se calculó la media geométrica de las respuestas espectrales, que al igual que las respuestas calculadas en el paso anterior serán una función del ángulo rotacional y del período para un valor fijo de amortiguamiento:
 (2)
(2)
f) Se ordenan los valores de GM (ϴ ,T ) para un valor fijo de Ti, de menor a mayor, conformando una matriz con los valores para cada período considerado.
g) Finalmente se obtiene la medida GMRotDpp, correspondiente a la media geométrica GM según el percentil deseado para cada período, se utilizan los percentiles 0, 50 y 100, que corresponden al mínimo, mediana y máximo.
3.1.2 GMRotIpp
A continuación se detalla el procedimiento que se utilizó para el cálculo de la GMRotIpp.
a) Para este cálculo partimos de la medida GMRotDpp. Esta medida se computa para el rango de períodos útil para cada registro, el cual se ha definido de acuerdo a las frecuencias del filtro aplicado por los centros sismológicos a cada archivo.
b) Para cada período, se normaliza el conjunto de medias geométricas de la ecuación 2 para todos los ángulos de rotación respecto a GMRotDpp.
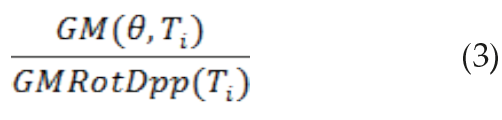
c) A continuación se calcula la función de penalización o de error, definida por la ecuación:
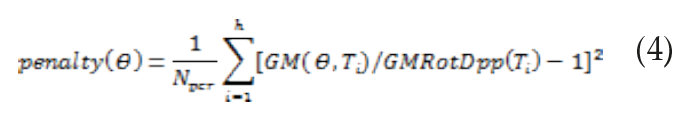
Donde el rango de periodos se extiende de T1 a Th (dependiente de la frecuencia mínima de filtrado suministrada en cada registro). GM (θ, Ti) es la media geométrica del espectro de respuesta para el período Ti computado para el ángulo de rotación θ, y GMRotDpp (Ti) es el valor del percentil de GM (θ, Ti) sobre todos los ángulos de rotación posibles, como se definió previamente.
d) Se encuentra el ángulo de rotación correspondiente al mínimo de la función de penalización, ϴmin. La figura 1 muestra el cálculo de la función de penalización para el percentil 50.
e) Como ya se habían calculado los espectros de respuesta para el rango de rotaciones de interés en el cálculo del GMRotDpp, se selecciona el espectro correspondiente al ángulo mínimo de la función de penalización (ϴmin). Al espectro de respuesta resultante se le llama GMRotIpp, definido por:
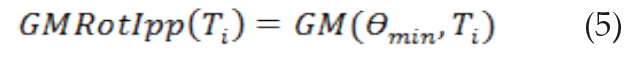
La selección de ϴmin busca evitar variaciones extremas lejos del valor del percentil deseado para todos los períodos. En particular, para GMRotI50 el procedimiento evita valores muy bajos de medias geométricas asociadas con movimientos fuertemente correlacionados.
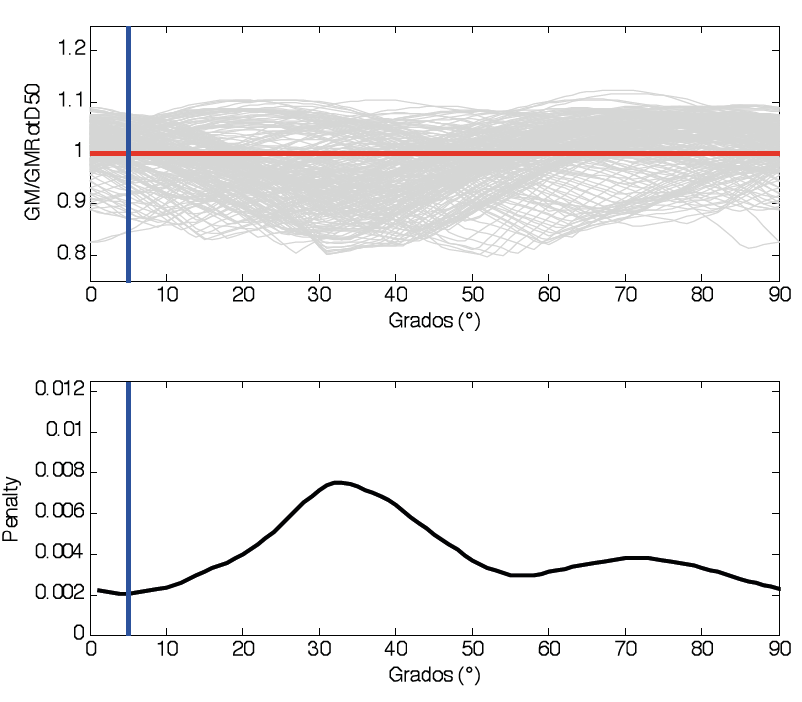
Figura 1. Cálculo de la normalización de GM/GMRotD50 necesaria para el cálculo de la función de penalización y debajo la función de penalización para el cálculo del θmin para el percentil 50. La línea azul que atraviesa ambas figuras muestra el ángulo que minimiza la función de penalización.
3.2. Media Cuadrática de Espectros de Respuesta y RotD100
La media cuadrática (QM) representa la orientación del sensor, por lo que no existe la necesidad de rotar la señal para obtener la respuesta máxima [11]. Por lo que su cálculo es muy simplificado si se utiliza la siguiente ecuación:
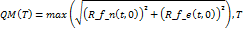 (6)
(6)
donde es la historia temporal de la respuesta del osciladordeungradodelibertadenladirección N-S, debido a la aceleración y, sería la correspondiente respuesta para la aceleración .
Boore [12] define la medida RotD100, la cual resulta equivalente a la media cuadrática [11]. Esta medida representa el valor máximo de aceleración espectral (Sa) para cada oscilador de un grado de libertad, al considerar los espectros rotados para una componente horizontal.
Siguiendo la metodología aplicada para el cálculo de las medidas GMRotDpp y GMRotIpp, una vez que se han calculado todos los espectros con la rotación de la señal, se seleccionan los valores máximos de la aceleración espectral Sa en función del período (Tn), y así se obtiene el espectro correspondiente al percentil 100, que será igual al valor obtenido con la media cuadrática [12].
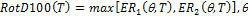 (7)
(7)
4. Resultados
Los resultados que se presentan a continuación, reflejan el comportamiento de la base de datos completa, sin hacer distinción entre países o tipos de suelo. Para resultados más detallados se puede consultar el estudio de Pinzón-Ureña [13].
4.1 Promedio de los espectros de respuesta
Una vez seleccionados los registros de aceleración, se realizó el cálculo de los espectros de respuesta en aceleración, descritos en la sección anterior, con lo que se procedió a calcular el promedio de los espectros para cada medida de intensidad.
Para poder calcular los promedios para cada medida de intensidad, fue necesario normalizar los espectros con respecto al PGA, con el fin de eliminar la dependencia con respecto a esta variable. Durante la normalización se utiliza el PGA de la media geométrica sin rotar, para evitar una disminución de la amplitud de los espectros que originaría normalizar con respecto al PGA de cada medida, además de considerar relevante examinar las diferencias que se presentan en comparación entre las nuevas medidas y la GM sin rotar. Al valor obtenido luego de la normalización, se le conoce como el factor espectral dinámico (FED). A continuación se expresa la forma matemática de las normalizaciones aplicadas.
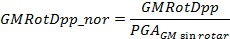 (8)
(8)
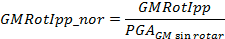 (9)
(9)
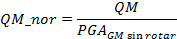 (10)
(10)
 (11)
(11)
Para el cálculo de promedios de los espectros normalizados, se realizó un análisis comparativo entre la media aritmética y la media geométrica de los espectros, con el fin de definir qué media utilizar. La media geométrica se define como la raíz enésima (siendo n el número de registros), de la multiplicación de los valores de aceleración de los espectros de respuesta normalizados (Sa_nor), o lo que es igual, el antilogaritmo del promedio de los logaritmos naturales de la respuesta espectral normalizada calculada para cada medida de intensidad [14] y la media aritmética se define como la suma de todos los valores de aceleración de los espectros de respuesta normalizados para cada período, dividido entre el número de registros.
Se tomó el vector del período de 1 segundo de los espectros de respuesta para todos los sismos calculados con la medida GMRotI50, con el fin de comparar la distribución de aceleraciones espectrales normalizadas (Sa_nor). Al comparar el histograma de Sa_nor, el cual representa la distribución de los valores en escala natural, con el de ln(Sa_nor), que representa los valores en escala logarítmica se infiere que la media aritmética posee una distribución sesgada a la izquierda, mientras que con la media geométrica se obtiene una distribución normal con el logaritmo de los valores, que es equivalente a una distribución log- normal).
La distribución obtenida con los valores en escala logarítmica, se ajusta a las teorías empleadas a la hora de ajustar las ecuaciones del movimiento del suelo [15][16], que se considera se ajustan a una distribución de probabilidades log-normal, por lo que se considera la media geométrica un mejor estimador de los valores promedios para el caso de medidas de intensidad sísmica.
4.2 Comparación de la media geométrica si rotar, GMRotDpp, GMRotIpp
Para comparar las medidas, se realizó un cálculo masivo de los 1406 registros seleccionados, utilizando un programa desarrollado en MATLAB. Primero se calculó la respuesta espectral en aceleración de todos los registros para todas las combinaciones lineales consideradas con la variación del ángulo de giro. Posteriormente se calcularon las diferentes medidas independientes de la orientación del sensor, siguiendo la metodología descrita anteriormente.
De los 1406 acelerogramas seleccionados, se calculó la respuesta espectral para cada componente horizontal y sus respectivas rotaciones, esto para osciladores de un grado de libertad con un rango de 133 a 200 períodos por señal, dependiendo del Th. Una vez calculados los espectros de respuesta para los 90 grados de rotación considerados para cada componente, se procedió a calcular la media geométrica y la media cuadrática de ambas componentes. Esto conlleva un cálculo computacional de 253080 espectros de respuesta en total.
Una vez calculados todos los espectros de respuesta se determinaron las diferentes medidas de interés (GMRotD50, GMRotD100, GMRotI50, GM Sin Rotar y QM). Se obtuvieron 1406 espectros de respuesta por medida, que representan a cada uno de los acelerogramas seleccionados. Posteriormente se normalizaron los espectros con el PGA de la media geométrica sin rotar, con el fin de obtener un promedio de todos los espectros para cada medida. Tal y como se explicó en la sección anterior los promedios fueron determinados con la media geométrica y cuando se hable de espectros promedio, se debe hacer referencia a este concepto. En la figura 2a se muestra una comparación de las proporciones (ratio) de la GMRotI50 con respecto a la GMRotD50 y la media geométrica sin rotar. Se observa que la medida dependiente del período (GMRotD50) se asemeja mucho a la independiente (GMRotI50), en cambio, existe una mayor variación entre la GMRotI50 y la media geométrica de la señal sin rotar. Se observa además en esta figura que para casi todo el rango de períodos considerados, la GMRotI50 es, en promedio, mayor que la GMRotD50 y la GM sin rotar, lo cual podría indicar que el proceso de selección de la medida independiente sobrevalora la respuesta en comparación a la medida dependiente, lo cual se aleja de la teoría pues el planteamiento busca que ambas medidas sean lo más parecidas posible.
Para el cálculo de los ratios se utilizó el antilogaritmo del promedio de los logaritmos naturales de la proporción de las medidas que se querían comparar, lo cual representa la media geométrica de los ratios [14]. De la misma forma se calcularon las desviaciones típicas (estándar).
En la figura 2b se muestran los resultados obtenidosque las mostradas en la figura 2a, pero para una base de datos distinta. Se observa que se obtuvieron resultados similares, ya que en ambos casos la relación GMRotD50/GMRotI50 es muy cercana a 1, en cambio la GM Sin Rotar/GMRotI50, se aleja entre un 1 y 2% aproximadamente.
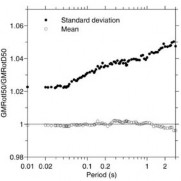
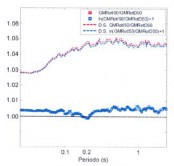
La relación GMRotI50/GMRotD50 se comparó con los resultados publicados por Boore et al. [6], pues utilizaron una metodología distinta para el cálculo de los ratios. Los valores mostrados en la figura 3a no reflejan el logaritmo inverso del promedio de los logaritmos, en cambio, sumaron 1.0 a los promedios de los logaritmos naturales de las proporciones, para convertirlos directamente en factores de multiplicación. De esta forma, en la figura 3b, se observa que no existe una gran diferencia para el promedio de las relaciones, siempre y cuando los valores de los del promedio de los logaritmos sean cercanos a cero, como es el caso de los ratios calculados. Por otro lado, para el caso de las desviaciones estándar sí se observa una gran diferencia con respecto a la metodología de Boore et al. [6].
a 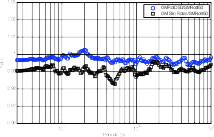
b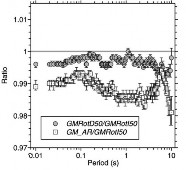
Figura 2. (a) Comparación de los ratios GMRotD50/GMRotI50 y (b) GM Sin Rotar/GMRotI50 con respecto a los obtenido por Boore [12].
En las figuras 2 y 3, se observa que esta relación presenta ratios entre 1.00 y 1.01, lo que muestra que la variación entre ambas es de menos de 1 %. De igual forma ocurre con la media geométrica sin rotar, la cual sólo para algunos períodos supera el 2 % de diferencia con respecto a la GMRotI50.
Siguiendo la misma metodología con la que se obtuvieron las relaciones anteriores, se compararon los valores de GMRotD100 con respecto a los de GMRotD50, GMRotI50 y la GM sin rotar (figura 4). Se encontraron variaciones entre el 5 y 6 % para la GMRotI50, 6 y 7 % para la GMRotD50 y entre 7 y 8 % para la GM sin rotar.
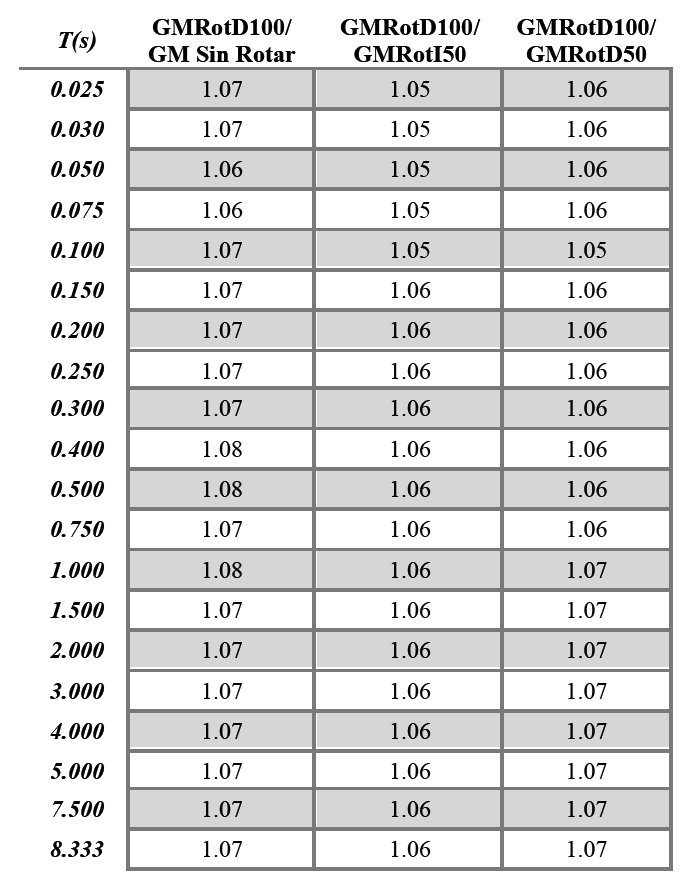
Los valores mostrados en la tabla 1 fueron calculados para períodos específicos, con el objetivo de condensar la información disponible. Estas relaciones pueden utilizarse para obtener el valor de la GMRotD100 a partir de cualquiera de las otras medidas, utilizándolas como factores multiplicativos [1].
 a
a
 b
b
Figura 3. (a) Comparación de los ratios GMRotI50/GMRotD50 obtenidos por Boore et al. [6] y (b) GMRotI50/GMRotD50 obtenidos en esta investigación.
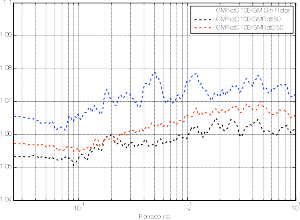
Figura 4. Comparación de los ratios GMRotD100/GM Sin Rotar, GMRotD100/GMRotI50 y GMRotD100/GMRotD50.
Tabla 1. Valores de las relaciones GMRotD100/GM Sin Rotar, GMRotD100/GMRotI50 y GMRotD100/GMRotD50 para diferentes períodos.
4.3 Comparación con la media cuadrática
Una vez comparadas las medidas independientes a la orientación del sensor, se decidió comparar las mismas con la media cuadrática (QM). Esta medida representa la máxima respuesta espectral de un registro de aceleraciones, independiente a la orientación en que se haya registrado el evento [11].
Al comparar los ratios de la media cuadrática con respecto a la GMRotD50, GMRotI50 y la GM sin rotar, se observa que la relación no es lineal a lo largo del rango de períodos considerado, ver figura 5. Existen variaciones entre un 21 y un 29 % con respecto a la GMRotI50, 21 y 30 % con la GMRotD50 y 22 y 30 % con la media geométrica sin rotar. En la Tabla 2 se muestra el valor de las relaciones para un conjunto de períodos específicos, con estos valores se puede calcular la media cuadrática directamente si se tiene el valor de cualquiera de las medidas relacionadas.
La relación QM/GMRotI50, fue comparada con las obtenidas por Beyer & Bommer [1], Huang & Whittaker [17], Watson-Lamprey & Boore [18], Campbell [19] y NEHRP [20]. Para el caso de la relación de Huang & Whittaker [17], se grafican tanto la relación para sismos cercanos (NF) como la relación para sismos de campo lejano (FF).
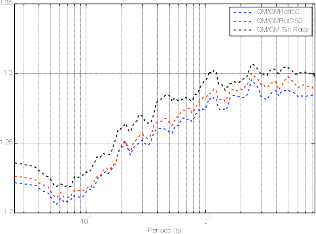
Figura 5. Comparación de los ratios QM/GMRotI50, QM/ GMRotD50 y QM/GM Sin Rotar.
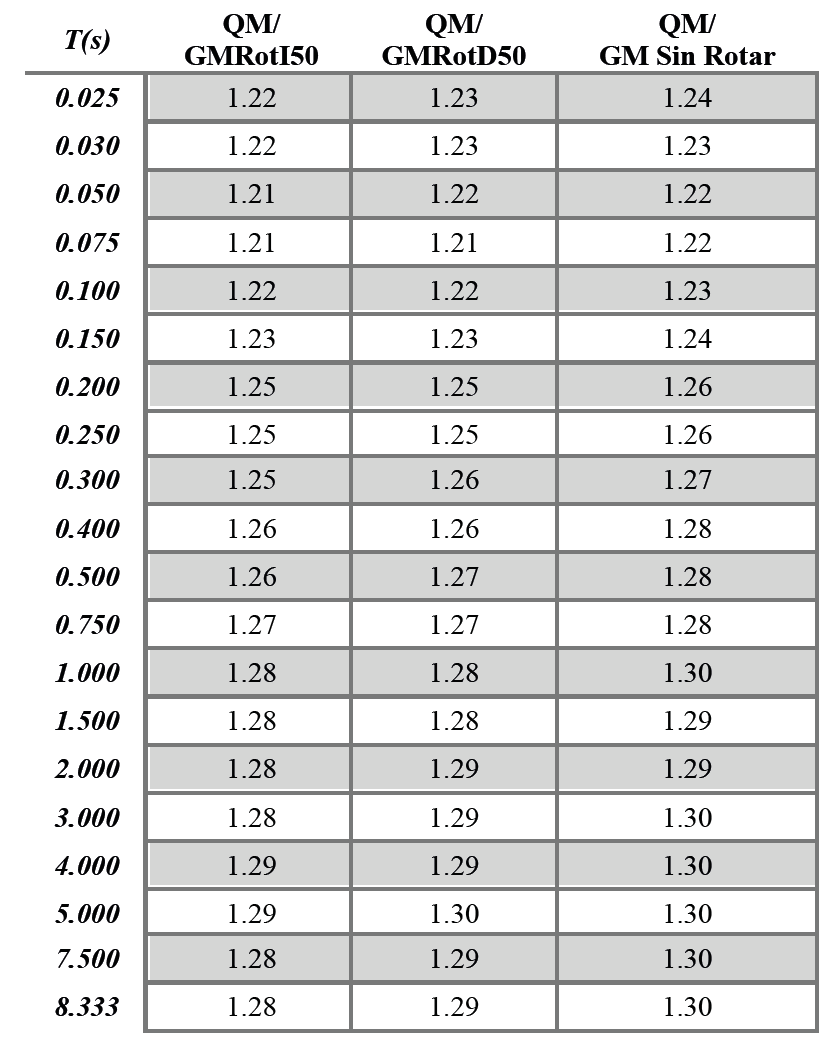
Tabla 2. Valores de las relaciones QM/GM Sin Rotar, QM/GMRotI50 y QM/GMRotD50 para diferentes períodos.
Como se observa en la figura 6, se obtuvieron valores similares a los de las investigaciones mencionadas. Para todos los casos (con la excepción de la expresión propuesta por el NEHRP [20]) la relación inicia constante para períodos bajos, con valores cercanos a 1.20, aumentando de manera lineal para períodos medios, para volverse constante de nuevo en períodos largos con un valor aproximado de 1.30.
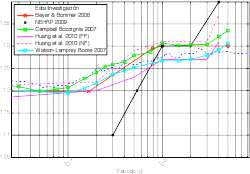
Figura 6. Comparación de la relación QM/GMRotI50 obtenida para esta investigación con respecto a las de otros autores.
4.4 Comparación con espectro de respuesta tipo código
Este apartado muestra el cálculo de los espectros medios para las medidas de intensidad, descritas en las secciones anteriores, esto para cada tipo de suelo y país, para posteriormente compararlos con los espectros de diseño del Código Sísmico de Costa Rica 2010 [21]. En este código, se definen las características tanto dinámicas como mecánicas, empleadas para la clasificación del tipo de suelo, aplicado por Schmidt-Díaz [22], para la base de datos empleada en esta investigación.
En la figura 7, se muestran los resultados obtenidos del cálculo masivo de registros de Costa Rica, con las medidas GMRotD50, GMRotI50, GMRotD100 y la media cuadrática, para un tipo de sitio S1.
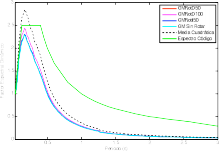
Figura 7. Comparación de los promedios calculados para cada medida de intensidad para todos los registros de Costa Rica.
La línea verde representa el espectro elástico de código (5 % de amortiguamiento). Se observa que el promedio calculado se ajusta bastante bien al espectro del código y que la media cuadrática supera las otras medidas, siendo ésta la única medida que supera claramente el espectro del código para periodos bajos.
5. Conclusiones
Se presentan aquí las principales conclusiones con especial énfasis en el análisis de direccionalidad.
La ventaja teórica de las medidas de intensidad basadas en la media geométrica de las componentes horizontales, es que eliminan los efectos de la orientación del sensor como contribuyente a la incertidumbre aleatoria de las medidas. Estos resultados son de gran interés en el desarrollo de ecuaciones predictivas del movimiento del suelo como son las leyes de atenuación en estudios de peligrosidad sísmica.
Aunque este tipo de estudios requieren un esfuerzo computacional alto cuando se compara con el uso de la media geométrica correspondiente a las componentes horizontales sin rotar, actualmente se dispone de programas y equipos informáticos que permiten abordar el problema de forma eficiente.
La GMRotI50, es en general, mayor que la GMRotD50 y que la GM sin rotar.
Un aspecto a mejorar de la metodología de cálculo de GMRotIpp, es que se requiere la selección de un rango de períodos para su computación y los resultados de la función de penalización pueden cambiar de acuerdo a la cantidad de períodos y la forma en que estos se distribuyen dentro del rango seleccionado. En este sentido sería conveniente definir funciones de penalización y, en consecuencia GMRotIpp por rangos de períodos.
Se han obtenido resultados similares a los obtenidos por Boore et al. [6] y Boore [12]; las relaciones entre GMRotD50 y GMRotI50, que en general son muy cercanas a la unidad, mientras que el valor de la GM Sin Rotar tiene una variación cercana al 1 % respecto al GMRotD50 y GMRotI50. A pesar de que existe una diferencia pequeña entre la GMRotD50, GMRotI50 y la GM sin rotar, es recomendable utilizar las medidas independientes de la orientación ya que disminuyen la incertidumbre epistémica en las leyes de predicción de movimiento del suelo [1]. Este tipo de análisis requiere recalcular los factores de regresión de las leyes de atenuación usando la misma base de datos, por lo que queda fuera de alcance de este estudio.
Comparando los valores obtenidos con la media cuadrática (QM) con los correspondientes a la media geométrica sin rotar y teniendo en cuenta que éste último es el valor empleado en las leyes de atenuación actuales, se estima que se puede llegar a subestimar la demanda entre un 20 y un 30 %.
Al comparar la medida GMRotD100 con respecto a las GMRotD50, GMRotI50 y la GM sin rotar se han hallado variaciones en la demanda entre el 5 y 6 % con respecto a la GMRotI50, 6 y 7 % con respecto a la GMRotD50 y entre 7 y 8 % con respecto a la GM sin rotar. Lo que demuestra que la demanda se puede llegar a subestimar entre un 7 y 8 % en las leyes de atenuación actuales.
Fue posible determinar factores multiplicativos, que pueden ser utilizados para esta base de datos específica, con el fin de transformar, de manera aproximada, las aceleraciones espectrales de una medida a otra, sin necesidad de realizar todos los cálculos masivos nuevamente y, en consecuencia, sin necesidad de recalcular las leyes de atenuación. El cálculo de los máximos de la media cuadrática de la respuesta (QM), puede considerarse como la máxima respuesta posible, correspondiendo al caso más desfavorable. En consecuencia, estos valores, se pueden utilizar para el diseño o evaluación del riesgo de estructuras de especial importancia como por ejemplo edificios de patrimonio histórico- cultural u otras construcciones de alto riesgo, ya que se puede calcular el valor máximo para la base de datos disponible y esta envolvente se puede considerar que corresponde a un sismo de gran período de retorno, al representar el percentil 100 de todos los espectros posibles para la base de datos disponible. Esta aplicación debe ser comparada con los estudios de peligrosidad sísmica, para verificar si existen valores espectrales mayores a los determinados con el procedimiento propuesto y ser conscientes de que, en este caso, nos situamos del lado conservador.
Al realizar el análisis comparativo de los resultados con los espectros de diseño, se obtuvo un acuerdo razonable con los espectros de diseño situándose estos del lado conservador. Otro punto a recalcar es que, la única medida que supera los espectros de código es la media cuadrática (QM), y esto ocurre en el rango de períodos bajos. Sin embargo los valores del espectro de diseño muestran un buen acuerdo con la GM sin rotar. Este tipo de media corresponde a la mayoría de los estudios realizados hasta la fecha.
6. Agradecimientos
Para el desarrollo de este trabajo, fue fundamental el aporte de datos realizado por las siguientes instituciones:
- El Salvador: SNET (Douglas Hernández), UCA (Reynaldo Zelaya)
- Nicaragua: INETER (Emilio Talavera)
- Costa Rica: LIS (Aarón Moya y Victor Schmidt), ICE (Álvaro Climent)
De igual forma quisiéramos agradecer al Comité Editorial de la Revista I+D Tecnológico y al grupo de Evaluadores por su atención y comentarios.
Referencias Bibliográficas
[1] Beyer K., Bommer J.J. (2006) Relationships between Median Values and between Aleatory Variabilities for Different Definitions of the Horizontal Component of Motion. Bull Seism. Soc. Am. 96(4A):1512–1522. doi: 10.1785/0120050210.
[2] Douglas J (2003) Earthquake ground motion estimation using strong-motion records: a review of equations for the estimation of peak ground acceleration and response spectral ordinates. Earth-Science. Rev. 61(1-2):43–104. doi: 10.1016/S0012- 8252(02)00112-5.
[3] Boore D.M., Stewart J, Seyhan E, Atkinson GM (2013) NGA-West2 Equations for Predicting Response Spectral Accelerations for Shallow Crustal Earthquakes. 106.
[4] Abrahamson N.A., Shedlock K.M. (1997) Overview Seism. Res. Lett. 68(1):9–23. doi: 10.1785/gssrl.68.1.9.
[5] Spudich B.P., Chiou B.S.J., Graves R., et al. (2004) A Formulationof Directivity for Earthquake Sources Using Isochrone Theory. U.S. Geol. Surv. Open-File Rept. 2004-1268, 54pp.
[6] Boore D.M., Watson-Lamprey J., Abrahamson N.A. (2006) Orientation-independent measures of ground motion. Bull. Seism. Soc. Am. 96(4A):1502–1511. doi: 10.1785/0120050209.
[7] Bommer J.J., Abrahamson N.A., Strasser F.O., et al. (2004) The Challenge of Defining Upper Bounds on Earthquake Ground Motions. Seism. Res. Lett 75(1):82–95. doi: 10.1785/ gssrl.75.1.82.
[8] Schmidt Diaz, V. (2010). Avances para estudios del riesgo sísmico a escala regional y local: aplicación a América Central y a la Bahía de Cádiz (Sur de España). Universitat Politècnica de Catalunya. Retrieved from http://www.tdx.cat/ handle/10803/6273
[9] Laboratorio de Ingeniería Sísmica U de CR (2014) Descarga de Registros. http://www.lis.ucr.ac.cr.
[10] V. Schmidt, A. Dahle, and H. Bungum. Costa Rican spectral strong motion attenuation. Technical report, NORSAR, Kjeller, Norway, Nov. 1997. Reduction of Natural Disasters in Central America Earthquake Preparedness and Hazard Mitigation Phase II: 1996 2000, Part 2.
[11] Rupakhety R., Sigbjörnsson R. (2013) Rotation-invariant measures of earthquake response spectra. Bull. Earthq. Eng. 11(6):1885–1893. doi: 10.1007/s10518-013-9472-1.
[12] Boore D.M. (2010) Orientation-Independent, Nongeometric- Mean Measures of Seismic Intensity from Two Horizontal Components of Motion. Bull. Seism. Soc. Am. 100(4):1830– 1835. doi: 10.1785/0120090400.
[13] Pinzón-Ureña, L.A. (2014). Evaluación de medidas de intensidad del movimiento del suelo independientes de la orientación del sensor para una base de datos con acelerogramas de Costa Rica, El Salvador y Nicaragua. Universitat Politècnica de Catalunya. Retrieved from http://upcommons.upc.edu/ pfc/handle/2099.1/24352.
[14] Shahi S.K., Baker J.W. (2013) NGA-West2 Models for Ground- Motion Directionality, Tech. Rept. No. 2013/10, Pacific Earthquake Engineering Research Center, Berkeley, California, 46pp.
[15] Joyner W., Boore D.M. (1981) Peak horizontal acceleration and velocity from strong-motion records including records from the 1979 Imperial Valley, California, earthquake. Bull Seism. Soc. Am. 71(6):2011–2038.
[16] Abrahamson N.A., Youngs R. (1992) A Stable Algorithm for Regression Analyses using the Random Effects Model. Bull. Seism. Soc. Am. 82(1):505–510.
[17] Huang Y-N., Whittaker A.S., Luco N. (2011) Establishing Maximum Spectral Demand for Performance- Based Earthquake Engineering : Collaborative Research with the University at Buffalo and the USGS, USGS Tech. Rept. Award Number 08HQGR0017, U.S. Geol. Surv, Reston, VA.
[18] Watson-Lamprey J., Boore D.M. (2007) Beyond SaGMRotI: Conversion to SaArb, SaSN, and SaMaxRot. Bull. Seism. Soc. Am. 97(5):1511–1524. doi: 10.1785/0120070007.
[19] Campbell K.W., Bozorgnia Y. (2007) Campbell-Bozorgnia NGA Ground Motion Relations for the Geometric Mean Horizontal Component of Peak and Spectral Ground Motion Parameters, Tech. Rept. No. 2007/02, Pacific Earthquake Engineering Research Center, Berkeley, California.
[20] Building Seismic Safety Council. (2009). NEHRPRecommended Seismic Provisions for New Buildings abd Other Structures. FEMA P-750, 388. Retrieved from http://www.fema.gov/ media-library-data/20130726-1730-25045-1580/femap_750. pdf.
[21] CFIA (2011) Código Sísmico de Costa Rica 2010, Editorial Tecnológica de Costa Rica, Cartago, Cartago, 378pp.
[22] Schmidt-Díaz V (2011) Clasificación de suelos basada en el cálculo de razones espectrales en sitios donde se ubican estaciones acelerográficas de América Central. Casos de El Salvador, Nicaragua y Costa Rica. Rev Geológica América Cent 44(1):9–26.
(2)