Optimización en manufactura mediante la experimentación y modelos de regresión logística

Optimization in manufacturing through experimentation and logistic regression models

Armando Mares Castro^1*

¹ Facultad de Ingeniería Industrial, Instituto Tecnológico Superior de Purísima del Rincón, México

*Autor de correspondencia: [email protected]

Tipo de artículo: Original.
Recibido: 9 de enero de 2020.
Aceptado: 13 de julio de 2020.

DOI. https://doi.org/10.33412/idt.v16.2.2839

RESUMEN– En éste artículo se proponen tres esquemas de optimización para una respuesta de tipo fracción disconforme muestral en un proceso de manufactura. El diseño de experimentos es una técnica estadística que se aplica para mejorar la calidad del producto final. El uso de modelos de regresión logística se recomienda cuando se analiza la fracción disconforme muestral como parámetro de la calidad. A partir de los resultados del experimento se construye un modelo matemático con el fin de optimizar los parámetros del proceso. La metodología propuesta fue aplicada al proceso de vulcanización en la fabricación de suelas de hule. Se realiza un análisis comparativo de tres metodologías de optimización para evaluar el mejor resultado. Los niveles obtenidos en dos procedimientos fueron iguales y en el tercero se verificó una solución menos eficiente. La mejor solución se aplicó al proceso con una significativa mejora en el nivel de calidad del producto.

Palabras clave– Algoritmos Genéticos, Función de Deseabilidad, Proceso de fabricación de suela de hule, Programación Cuadrática Secuencial, Regresión Logística.

ABSTRACT– In this article, three optimization schemes are proposed for a response of sample non-conforming fraction type in a manufacturing process. The design of experiments is a statistical technique that is applied to improve the quality of the final product. The use of logistic regression models is recommended when analyzing the sample non-conforming fraction as a quality parameter. From the results of the experiment a mathematical model is constructed in order to optimize the process parameters. The proposed methodology was applied to the vulcanization process in the manufacture of rubber soles. A comparative analysis of three optimization methodologies is performed to evaluate the best result. The levels obtained in two procedures were the same and in the third one a less efficient solution was verified. The best solution was applied to the process with a significant improvement in the level of product quality.

Keywords– Genetic Algorithms, Desirability Function, Rubber sole process, Sequential Quadratic Programming, Logistic Regression.

1. Introducción

Un proceso de manufactura consiste en la transformación de materias primas en productos terminados, cuya finalidad es la de satisfacer una necesidad. Las etapas de un proceso de manufactura incluyen el diseño del producto, la selección de las materias primas y la secuencia de los procesos a través de los cuales es transformada la materia prima hasta la obtención de un producto que debe cumplir con una serie de requisitos de calidad.

La secuencia de operaciones se integra desde los métodos de manufactura, la planeación del proceso, ensamble, pruebas y aseguramiento de calidad. Actualmente, las empresas manufactureras que deseen competir deben enfocarse en el cumplimiento de las características de calidad en el producto, también llamado “Voz del cliente”. Los objetivos y responsabilidades que se deben cumplir en las áreas de manufactura se indican a continuación:

• - Un producto debe cumplir con los requerimientos de diseño, especificaciones y estándares.

• - Un producto debe realizarse de la forma más eficiente (económicamente), minimizando el uso de métodos complejos.

• - La calidad debe integrarse en cada una de las etapas de manufactura del producto, desde el diseño hasta el ensamble, lo cual es preferible a tener fallas en las pruebas de calidad posteriores a la manufactura.

  Las actividades de manufactura deben cubrir varios requerimientos, ya que el producto debe ser manufacturado de la manera más económica posible y con el uso de métodos amigables con el medio ambiente.

• - Deben implementarse nuevas estrategias sobre organización en manufactura, nuevos desarrollos de materiales, así como la implementación de métodos computacionales sobre producción e integración, los cuales deben ser evaluados de forma constante.

• - Una organización manufacturera debe intentar alcanzar de forma consistente los más altos niveles de calidad y productividad (uso óptimo de recursos, materiales, máquinas, energía, capital, mano de obra y tecnología.

El diseño de experimentos es una técnica de estadística ampliamente utilizada para la mejora de los procesos a través de la obtención de los parámetros óptimos del proceso que generen una mejor calidad en el producto [1]. El muestreo por atributos del tipo pasa- no pasa es muy utilizado en manufactura para la clasificación del producto como conforme/ no conforme. Autor [2] presentaron una propuesta de análisis para datos de tipo discreto en un proceso de manufactura de suela de poliuretano, en la cual se logró la reducción del porcentaje de defectos mediante la aplicación de un diseño experimental tipo Taguchi y la optimización de una medida de desempeño independiente de ajuste (PERMIA).

Para el modelado de la respuesta se ajusta un modelo de regresión de tipo lineal o cuadrático. El propósito de los modelos es el estudio de la relación entre k factores X = (X₁,…,X_k ) variables de control. Para el caso propuesto en éste artículo se utilizó un diseño central compuesto para modelos cuadráticos. Para el caso de dos factores y una respuesta se tiene:

• 

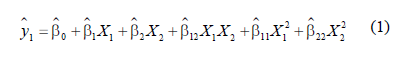
  El objetivo del esquema experimental es la reducción del porcentaje de defectos, o fracción disconforme muestral, a partir de la obtención de la mejor combinación de los niveles para los parámetros de control en un proceso. El problema de minimización puede ser analizado desde un esquema de optimización lineal o no lineal restringida sujeta a restricciones del área experimental permitida por el proceso, por ejemplo:

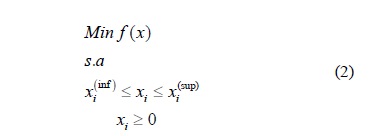
Donde f(x) se toma como el modelo estimado en (1), y las restricciones se definen en base al conocimiento del proceso. Un problema importante surge al analizar el modelo en (1), ya que se trata de un modelo de regresión ajustado que debe cumplir con los supuestos de independencia, normalidad y homoscedasticidad. Los supuestos no se cumplen en un modelo basado en proporciones, por lo cual se propone un análisis del modelo en el esquema de la regresión logística. El objetivo de éste artículo es la propuesta de tres esquemas de optimización aplicables al diseño experimental en manufactura. El caso de estudio trata sobre el proceso de fabricación de suela de hule y la reducción de defectos de tipo cualitativo que se detectan en la inspección del producto. La optimización se realiza mediante las técnicas de función de deseabilidad, Algoritmos Genéticos y Programación Cuadrática Secuencial.

2. Experimentación y Optimización

Las bases de la calidad mediante métodos estadísticos para la mejora y control de los procesos fueron definidas por autores como Shewhart, Fisher, Taguchi, entre otros. La ingeniería de calidad en el producto consiste en la aplicación de técnicas para la optimización de procesos en manufactura, a partir del diseño, la fabricación y el seguimiento del producto. La calidad ideal que un cliente puede esperar, es que el producto entregue el desempeño objetivo cada vez que éste sea utilizado para las operaciones destinadas a lo largo de su vida útil, sin efectos perjudiciales para el consumidor [4].

Dentro del tema de la calidad en el producto, el costo también es un factor importante. El problema de entregar un producto de calidad a bajo costo involucra a ingenieros, economistas, estadísticos y la gerencia. Se debe tomar en cuenta el costo de operación, el costo de manufactura, el costo de investigación y desarrollo del producto. La competencia actual en el mercado indica que las empresas solamente pueden sobrevivir si reducen los costos sin descuidar la calidad. La reducción de precios sin el sacrificio de los beneficios no es posible sin la mejora y el aseguramiento de la calidad en los productos y procesos.

Es importante analizar los efectos de la Mano de obra, Materiales, Métodos, Máquinas, Medio ambiente y Mediciones sobre las características críticas de la calidad para poder garantizar la calidad en el producto, para esto se requiere realizar pruebas y generar datos que proporcionen evidencias objetivas que permitan responder a las interrogantes planeadas por el experimentador sobre algún problema relacionado a la calidad en los productos y procesos. El diseño de experimentos consiste en determinar qué pruebas deben desarrollarse y de qué manera, para resolver problemas o lograr mejoras en la calidad.

1. 2.1 Proceso de fabricación de suela de hule

   El proceso de fabricación de suela de hule (figura 1), es un proceso de manufactura que involucra una serie de procesos físicos y químicos. La parte inicial del proceso involucra el pesado y mezclado de materias primas, tales como la goma elastomérica cruda, rellenadores base carbonato, silicatos, aceites, ácidos y químicos [5].

   El mezclado de los materiales se realiza en un molino especial denominado “Bámbury”, que trabaja con temperaturas y cuchillas especiales, el mezclado se realiza en un tiempo específico hasta obtener una mezcla de los materiales en forma de pasta. Posteriormente, se agregan a la pasta los pigmentos de color y aceleradores, éste proceso se realiza en máquinas de rodillos giratorios a través de los cuales se ingresa la pasta para formar láminas de material. Las tiras son llevadas a un área de ventilación para bajar la temperatura del material y aquí se cortan con suajes que tienen una forma similar a la suela.

   El siguiente proceso se considera el más importante: el vulcanizado de la suela, el cual se realiza en moldes que trabajan en base a 3 variables de control importantes: presión, tiempo y temperatura, con los cuáles se logra la forma final de la suela, que adquiere las propiedades características del producto. En ésta fase se realiza una inspección y selección por parte de los inspectores de calidad.

   Los procesos finales se realizan en el área de preacabado, en los cuales se realiza un rebabeado de la suela para retirar el material sobrante en los extremos de la suela. Se realiza también el cardado interno y externo para detallar el producto. El proceso final es un cepillado que mejora la vista de la suela. Aquí se realiza otra inspección de calidad antes de realizar el loteo final del producto.

   

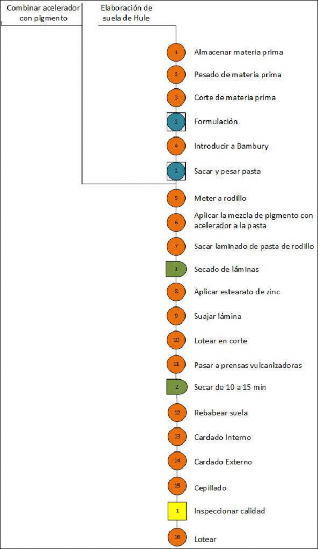
   Figura 1. Proceso de manufactura de la suela de hule para calzado.

2. 2.2 Diseño de Experimentos

   El diseño de experimentos es una metodología que se utiliza para conocer, estudiar e investigar procesos y productos en la industria. En éste artículo se propone el uso del diseño central compuesto (DCC), el cual se aplica cuando se tienen tres o más factores. El diseño DCC satisface propiedades estadísticas como la ortogonalidad y rotabilidad, lo cual lo hace un diseño eficiente en el análisis. Sus características pueden consultarse en [6,7,8].

   El DCC (figura 2), consta de un diseño factorial con puntos centrales. Al diseño se le agregan puntos adicionales llamados axiales o estrella, los cuales permiten estimar curvatura.

   

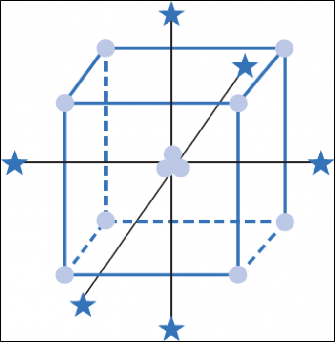
   Figura 2. Representación de un DCC para 3 factores.

   Con los resultados experimentales del diseño DCC se pueden ajustar modelos de regresión de segundo orden:

   

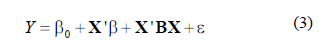
Donde X’ = (x₁,…,x_k) k factores, β₀ la constante, β₀ =(β₁,…, β_k) un vector de parámetros, B = (β₁₁,…, β_1k, β_k1,…, β_kk) matriz simétrica de parámetros de segundo orden y ε~N(0,σ²). El análisis de los residuales en cada modelo permite verificar la falta de ajuste, así como otras características relevantes.

2.3 Modelos de Regresión Logística

El modelo (3) es un modelo de regresión ajustado que debe cumplir con los supuestos clásicos en los residuales. Cuando se trabaja con respuestas de tipo proporciones se conoce de antemano que no se cumplirán los supuestos debido a que se trata de una variable aleatoria de Bernoulli, para éste caso, se propone el uso de modelos lineales generalizados [9,10]. Para el caso de estudio en particular, se aplica el modelo de regresión logística, el cual tiene mejor aplicación cuando las respuestas experimentales siguen una distribución Binomial o de Bernoulli, como lo es el caso de análisis para la fracción disconforme muestral.

En un modelo de regresión logística se considera que la respuesta toma valores entre 0 y 1, suponiendo que el modelo es:

Donde xi’=[1,xi1,xi2,…,xik], β’=[β0, β1, β2,…, βk] y la variable de respuesta yi toma valores entre 0 y 1. Se asume que la variable de respuesta yi es una variable aleatoria de Bernoulli con distribución de probabilidad P(yi=1)=πi si yi=1 y P(yi=0)=1- πi si yi=0. El valor esperado de yi es E(yi)=1(πi)+0(1- πi)= πi, dado que E(εi)=0. Así, de la ecuación (4) se tiene que E(yi)=xi ’β=πi. desde esta descripción, la varianza de yi se obtiene como ejemplo, σ2 yi = πi (1- πi), con lo que se demuestra que la media y la varianza están relacionados. En resumen, el modelo de regresión logística está en la forma de la distribución de Bernoulli y la variable yi es independiente en cada ensayo y valor esperado:

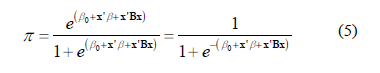
Los parámetros del modelo en (3) y (4) son estimados por el método de máxima verosimilitud. El modelo en (5) se reescribe como:

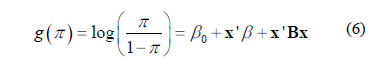
Así, la función de máxima verosimilitud se expresa como:

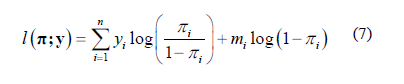
2.4 La función de deseabilidad

La función de deseabilidad fue introducida por E.C. Harrington Jr [11] y fue modificada por George Derringer & Ronald Suich [12]. La deseabilidad individual y la deseabilidad compuesta evalúan que tan bien una combinación de variables satisface los objetivos que se definieron para las respuestas. La deseabilidad individual evalúa la manera en la que la configuración optimiza una respuesta individual, mientras que la deseabilidad compuesta evalúa la manera en que la configuración optimiza un conjunto de respuestas en general. El rango de la deseabilidad es de 0 a 1, el valor de 1 indica la situación ideal mientras que 0 indica que una o más respuestas están fuera de los límites aceptables. La j- ésima respuesta se maximiza cuando el valor esperado Ŷ_i(x) sea igual al valor objetivo definido M_i,por lo que el valor decrecerá conforme se aleje del valor objetivo. Definiendo V_i y V_s como los valores extremos del proceso, solamente se aceptarán soluciones dentro del rango V_i≤ Ŷ_i(x)≤V_s y la función de deseabilidad di para cada una de las respuestas se define:

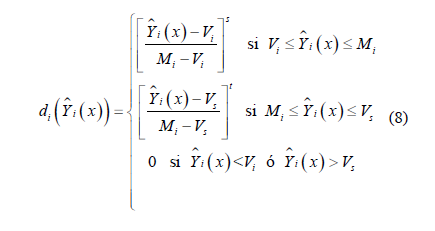
La ecuación (8) es llamada la transformación a dos lados, la cual aplica cuando la variable de respuesta Y_i tiene restricciones tanto mínimas como máximas, las cuales representan los niveles inferior y superior respectivamente para los factores experimentales. Las deseabilidades individuales son combinadas utilizando una media geométrica:

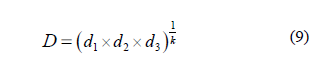
El valor para D representa la asignación de la deseabilidad combinada de los niveles de respuesta y es evidente que el rango de D estará entre 0 y 1. Una de las propiedades de D es que si alguna de las di=0 es decir, que una de las respuestas es inaceptable entonces D=0 y por lo tanto el producto global será inaceptable y (9) se reduce a una media geométrica.

2.5 Algoritmos genéticos

Dentro de las técnicas metaheurísticas de búsqueda, los algoritmos genéticos son técnicas computacionales adaptativas ampliamente utilizadas en problemas de optimización. La principal ventaja de los algoritmos genéticos sobre técnicas de optimización numérica tradicionales, tales como la programación no lineal [13], radica en que los algoritmos genéticos tienen una mayor probabilidad de encontrar el óptimo global particularmente cuando se utilizan funciones altamente no lineales, discontinuas, no diferenciables o estocásticas. Las bases de los Algoritmos genéticos fueron establecidas por E. C. Holland [14] y han sido analizadas también por otros autores como D. E. Goldberg [15].

Los Algoritmos Genéticos pueden ser utilizados para resolver problemas de optimización restringida o no restringida. La base de la técnica es la imitación del proceso de selección natural que sucede en la evolución biológica, el algoritmo cambia repetidamente una población de soluciones individuales en un proceso iterativo que involucra técnicas de selección, reproducción, mutación, crossover y migración. En su forma matemática las poblaciones son arreglos matriciales, un individuo puede aparecer en más de un renglón de la matriz y los individuos van cambiando a medida que se producen las nuevas poblaciones llamadas generaciones.

La función de fitness es la función que se desea optimizar y equivale a la función objetivo de un esquema de optimización tradicional. El algoritmo comienza con la creación de una población inicial aleatoria, en cada iteración se crean secuencias de nuevas generaciones que van evolucionando de acuerdo a las condiciones de optimización declaradas en el problema. La creación de una nueva población se realiza a través de la evaluación en la función de fitness, la cual es llamada puntuación de aptitud. Las evaluaciones de aptitud son escaladas para convertirlas en un rango de valores más adecuados llamados valores esperados, aquí se seleccionan los mejores individuos con el mejor valor de fitness llamados elite y pasan a la nueva población.

Para mejorar las siguientes generaciones, se producen los hijos de la elite por medio de cambios aleatorios a un padre single (mutación) o mediante la combi-nación de entradas de una pareja de padres (crossover), la población es reemplazada con los hijos para formar la siguiente generación. El algoritmo se detendrá cuando se cumple una condición de paro determinada por el analista.

2.6 Programación cuadrática secuencial

El algoritmo de programación cuadrática secuencial (PCS) es uno de los métodos más efectivos para la optimización no lineal restringida. Partiendo del problema de igualdad restringida:

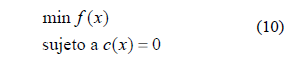
Donde c(x) es un conjunto de restricciones. La idea esencial del algoritmo PCS es modelar (10) en la iteración actual xk por un subproblema de programación cuadrática basado en una aproximación cuadrática de la función Lagrangiana:

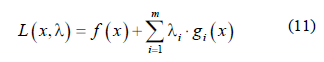
Aquí se simplifica suponiendo que las restricciones se han expresado como restricciones de desigualdad. Para obtener el subproblema de Programación Cuadrática, se linealizan las restricciones no lineales. El subproblema de programación cuadrática se define:

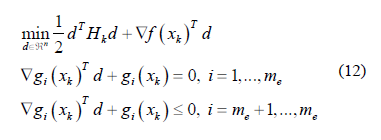
El subproblema 12 puede ser resuelto por cualquier técnica de programación cuadrática, la solución se utiliza para una nueva iteración:

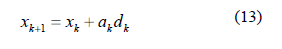
y utilizar el minimizador de éste subproblema para definir una nueva iteración xk+1. El reto es el diseño de un subproblema cuadrático que dé un buen paso para el problema de optimización restringida, y de ésta forma el algoritmo PCS presenta buena convergencia y buen desempeño práctico. El parámetro de longitud de paso ak se determina por un procedimiento de búsqueda para que se obtenga una disminución suficiente en una función de mérito.

La matriz Hk es una aproximación definida positiva de la matriz Hessiana de la función Lagrangiana (11), se puede actualizar con los métodos quasi- Newton, por ejemplo:

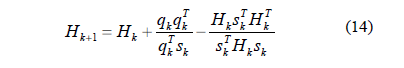
Donde

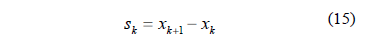
y

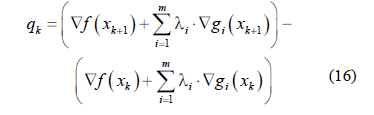
Los detalles del algoritmo PCS pueden ser consultados en [16].

3. Metodología

La propuesta de análisis (Figura 3), consiste en el análisis del proceso de suela de hule. Para cada una de las corridas experimentales se revisó la producción de todo un día en un molde específico y se revisó la calidad del lote total por parte de los inspectores de calidad, quienes clasificaron las suelas como conformes/ no conformes de acuerdo a los criterios de calidad predefinidos.

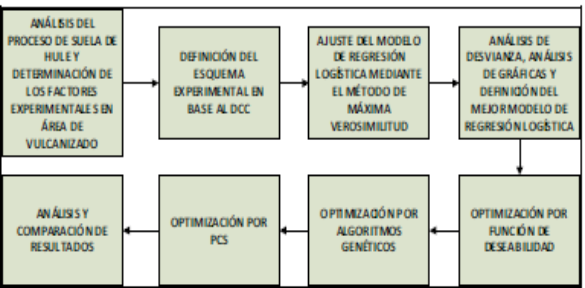
Figura 3. Metodología Propuesta.

El diseño experimental fue un DCC para tres factores con puntos estrella con 23 corridas experimentales. Se tomaron los tres factores de control en el proceso de vulcanizado de la suela (presión, temperatura y tiempo), que es el área en donde se genera la mayoría de los defectos de calidad. Los niveles del experimento (Tabla 1), fueron definidos por el personal de supervisión en base al conocimiento y experiencia del proceso.

Tabla 1. Factores experimentales y sus niveles

La matriz experimental y los resultados para las corridas se muestran en la tabla 2. El cálculo de la fracción disconforme muestral se define como p_i=x_i/n, donde p es el porcentaje de defectuosos de la muestra bajo el criterio pasa/ no pasa, x son las suelas clasificadas como defectuosas y n es la producción total del día en el molde seleccionado.

Tabla 2. Matriz experimental y resultados para las corridas

Una vez obtenidos los datos experimentales, se procede a realizar el análisis en el esquema de la regresión logística, como se puede observar, los valores de la respuesta están entre 0 y 1.

4.Resultados

4.1 Análisis de desvianza y modelo de regresión logística

En la tabla 3 se muestra el análisis de desvianza para el modelo de regresión logística, el R2 para el modelo completo es de 48.59%, el R2 adj es 30.75%. El valor P para la desvianza es de 0.035, al ser menor a α= 0.05 se indica que existe una relación estadísticamente significativa entre las variables con un nivel de confianza del 95%.

Tabla 3. Análisis de desvianza

Los estadísticos del modelo completo indican que se puede obtener un mejor modelo al eliminar términos que no son significativos, como se observa en la tabla 3, algunos términos muestran P valores mayores a α= 0.05, se aplica la selección de términos hacia atrás con la finalidad de mantener en el modelo los términos más significativos mientras que mejore el Valor P del modelo, los resultados se muestran en la tabla 4:

Tabla 4. Análisis de desvianza para el mejor modelo.

El análisis de desvianza para el modelo reducido muestra un valor P= 0.0002, que indica que el modelo con ajuste significativamente mejor que el modelo completo, el valor de R2 para el modelo reducido es de 47.91%, el R2 adj es 38%, el cual aumentó con relación al del primer modelo, lo cual indica que fue conveniente la eliminación de los elementos mediante el algoritmo de selección del paso hacia atrás.

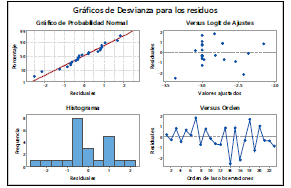
Figura 3. Análisis para los residuos en el modelo.

El análisis para los residuos en el modelo indica un buen comportamiento en cuanto a normalidad en los datos, la independencia y varianza constante muestran un comportamiento aleatorio, sin ciclicidad aparente, tendencias marcadas ni formas de embudo, por lo que se considera que se cumplen adecuadamente. Los términos X1 y X2 están presentes en interacciones seleccionadas por el algoritmo stepwise, con el fin de mantener un modelo jerárquico y debido a que dichos términos son necesarios en la optimización se regresan al modelo, quedando el valor P= 0.0022, el valor de R² para el modelo reducido es de 48.42%, el R2 adj es 34.55%, quedando el modelo:

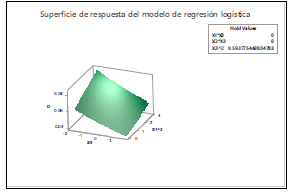
Figura 4. Superficie de respuesta del modelo de regresión logística.

En la figura 4 se muestra una vista de la superficie de respuesta para el modelo (17) para una de las parejas de elementos presente, se detecta curvatura por el efecto de los términos cuadráticos en el modelo, así como el efecto del ajuste al modelo logit.

4.2 Optimización por función de deseabilidad

Para la aplicación del esquema de optimización se busca la minimización de la respuesta fracción disconforme muestral, las restricciones se reducen al área experimental definida por los niveles codificados -1 a 1, que según la experiencia de los supervisores es la mejor región de operación para los valores reales de la temperatura, presión y tiempo definidos previamente en la tabla 1.

El esquema de optimización para la fracción disconforme muestral queda:

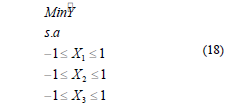
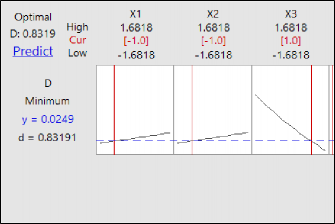
Figura 5. Gráfico de optimización por función de deseabilidad.

Tabla 5. Solución optimización por función de deseabilidad

Se observa en los resultados de la tabla 5 y figura 5 la convergencia en los niveles bajos para la temperatura y presión, lo cual significa la necesidad de trabajar la vulcanización de la suela en 140°C y 1400 psi respectivamente, mientras que el tiempo ideal de proceso se indica en nivel alto -8 minutos.

4.3 Optimización por Algoritmos Genéticos

Para la optimización por algoritmos genéticos se toma el mismo esquema de optimización que en (18), la función de fitness a minimizar es la función en (17) y los límites del proceso son los mismos que los utilizados en la función de deseabilidad. Los parámetros de inicio para la corrida del algoritmo se muestran en la Tabla 6.

Tabla 6. Parámetros de inicio para el algoritmo

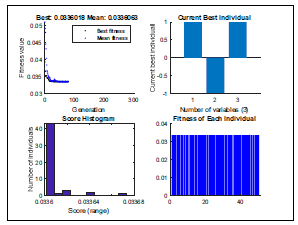
Figura 6. Gráfico de optimización por Algoritmos Genéticos.

Tabla 6. Solución por Algoritmos Genéticos

La solución para el algoritmo genético se puede observar en la figura 6 y tabla 6. El valor de la función de fitness quedó en 0.033606, los niveles óptimos para Temperatura y Tiempo fueron en nivel alto, 190°C y 8 minutos respectivamente, mientras que la presión se debe manejar en nivel bajo, 1400 psi. La convergencia del algoritmo se da en la generación 78. Se realizaron 30 corridas para verificar la convergencia del resultado, obteniéndose los mismos valores.

4.4 Optimización por Algoritmo PCS

El algoritmo PCS también se maneja dentro del esquema de optimización en (18), la función a minimizar es la misma que en 17 y el área experimental está definida por los límites de operación del proceso.

La solución del algoritmo se muestra en la figura 7 y tabla 7.

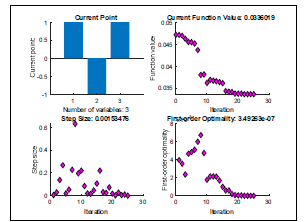
Figura 7. Gráfico de optimización por Algoritmo PCS.

Tabla 7. Solución por Algoritmo PCS

La convergencia del Algoritmo se da en la iteración 25, las soluciones son las mismas que con los Algoritmos Genéticos, así como el valor de la función = 0.033606. los niveles óptimos para Temperatura y Tiempo fueron en nivel alto, 190°C y 8 minutos respectivamente, mientras que la presión se debe manejar en nivel bajo, 1400 psi.

4.5 Comparativo de los métodos de optimización

Tabla 8. Comparativo de las soluciones por los 3 métodos

La referencia de la fracción disconforme muestral del proceso para el modelo de suela analizado era de 9% aproximadamente, el resultado obtenido por Algoritmos genéticos y por PCS presentaron una reducción de la fracción disconforme muestral por arriba del 5%, con el fin de verificar los resultados se realizaron 10 corridas de verificación con los niveles óptimos obtenidos por Algoritmos genéticos y por PCS. Los estadísticos se muestran en la tabla 9.

Tabla 9. Intervalos de confianza para las corridas de verificación

Se observa que, en las corridas de verificación, los intervalos de confianza contienen al valor óptimo obtenido por los algoritmos.

5. Conclusiones y discusión

En el caso de estudio presentado en éste artículo se presentó una comparación de la eficiencia de tres métodos de optimización aplicables a la experimentación dentro de los procesos de manufactura, adicionalmente se propuso el uso de la regresión logística como opción para el modelado de respuestas del tipo fracción disconforme muestral.

Los tres esquemas de optimización se pueden trabajar dentro de la optimización restringida y son compatibles para los problemas que se presentan dentro de la experimentación industrial. El algoritmo genético se perfila como la mejor opción de análisis cuando se tienen respuestas altamente no lineales, debido a que se tiene una mayor probabilidad de encontrar el óptimo global. El algoritmo PCS obtuvo la misma solución que el algoritmo genético, pero se puede presentar el problema de convergencia en óptimos locales, con lo cual se puede llegar a conclusiones apresuradas sobre la mejora del proceso.

El método de la función de deseabilidad presenta una mejor aplicabilidad cuando se analizan esquemas de multirespuestas en el experimento, con la finalidad de obtener soluciones de compromiso para problemas de tipo multiobjetivo, también se tiene la posibilidad de ponderar la importancia de cada una de éstas respuestas con la finalidad de generar una solución que cumpla mejor con los objetivos de la optimización.

Las corridas de verificación con los niveles óptimos obtenidos presentaron buenos resultados. Es recomendable la aplicación del diseño experimental en los procesos de manufactura con la finalidad de lograr los objetivos de calidad en el producto final, siendo una herramienta poderosa que no representa una inversión alta para su aplicación y por el contrario, se puede obtener buena utilidad por la mejora de la calidad.

Lo optimización de procesos dentro del esquema experimental es un área que requiere investigación, la presente propuesta se puede expandir a otros casos multirespuesta y dentro del diseño robusto de parámetros.

6. Referencias

[1] Box, G. E. P., Hunter, J. S., & Hunter, W. G. (2005). Statistics for Experimenters: Design, Innovation, and Discovery,2nd Edition.
[2] Book. https://doi.org/10.1080/00401706.1979.10489788 [2] Autor. (2015).
[3] Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to linear regression analysis. Introduction to Linear Regression Analysis (5th ed.). Wiley.
[4] Phadke, M. S., & Shridhar, M. (1989). Quality engineering using robust design. Prentice Hall.
[5] Ciesielski, A. (1999). Castable Polyurethanes. An Introduction to Rubber Technology.
[6] Draper, N. R. (1982). Center Points in Second-Order Response Surface Designs. Technometrics, 24(2), 127. https://doi.org/10.2307/1268490
[7] Box, G. E. P., & Draper, N. R. (1987). Empirical model-building and response surfaces. Wiley.
[8] Khuri, A. I., Cornell, J. A., & Cornell, J. A. (2018). Response Surfaces: Designs and Analyses. Routledge. https://doi.org/10.1201/9780203740774
[9] McCullagh, P. (Peter), & Nelder, J. A. (1989). Generalized linear models. Chapman and Hall.
[10] Hamada, M., & Nelder, J. A. (1997). Generalized Linear Models for Quality-Improvement Experiments. Journal of Quality Technology, 29(3), 292–304. https://doi.org/10.1080/00224065.1997.11979770
[11] Harrington, E. C. (1965). The desirability function. Industrial Quality Control.
[12] Derringer, G., & Suich, R. (1980). Simultaneous Optimization of Several Response Variables. Journal of Quality Technology, 12(4), 214-219. https://doi.org/10.1080/00224065.1980.11980968
[13] Nocedal, J., & Wright, S. J. (2006). Numerical optimization. Springer.
[14] Holland, J. H. (1984). Genetic Algorithms and Adaptation. In Adaptive Control of Ill-Defined Systems. https://doi.org/10.1007/978-1-4684-8941-5_21
[15] Goldberg, D. E. (David E., & E., D. (1989). Genetic algorithms in search, optimization, and machine learning. Addison-Wesley Longman Publishing Co., Inc. Retrieved from https://dl.acm.org/citation.cfm?id=534133
[16] Fletcher, R. (2000). Practical Methods of Optimization. John Wiley & Sons, Ltd. https://doi.org/10.1002/9781118723203