Diseño e implementación de un generador eléctrico lineal en la suspensión de bicicletas
Design and implementation of a linear electrical generator in bicycle suspension
Jahir Argote 1*, Arianne Troudart 1, César Moreno 1, Daniel De Los Ríos 1 Arthur James 2
1 Facultad de Ingeniería Eléctrica, Universidad Tecnológica de Panamá
2 Facultad de Ingeniería Mecánica, Universidad Tecnológica de Panamá
https://doi.org/10.33412/rev-ric.v6.2.2893
Vol. 6 - N.° 2 · Diciembre · 2020
Resumen El obtener el mayor provecho de la energía en un sistema es un campo prioritario en el mundo de la ingeniería. Identificamos la posibilidad de aprovechar la energía liberada en el sistema de suspensión de medios de transporte terrestre y transformarla en forma de energía eléctrica. En este artículo se presentan resultados experimentales de la generación eléctrica al aprovechar las vibraciones de la suspensión de una bicicleta por medio del uso de un generador eléctrico lineal. Se propone un diseño y prototipo para acoplar el generador eléctrico lineal a bicicletas como un accesorio. Se construye el generador eléctrico lineal y el acople para realizarle pruebas previniendo obtener “efecto fin” en el voltaje generado. Finalmente, se extraen los datos experimentales de generación eléctrica y se encuentran resultados similares a las expectativas planteadas en un análisis teórico. Dichos resultados pueden ser utilizados para identificar posibles aplicaciones.
Palabras clave Bicicleta, efecto fin, generador eléctrico lineal, suspensión.
Abstract Getting the most out of the energy in a system is a priority field in the world of engineering. We identified the possibility of harnessing the energy released in the suspension system of land transport means and transforming it into electrical energy. This article presents experimental results of electrical generation by taking advantage of the vibrations of the suspension of a bicycle through the use of a linear electrical generator. A design and prototype are proposed to couple the linear generator to bicycles as an accessory. The linear generator and the coupling are built to carry our tests, preventing obtaining "end effect" in the generated voltage. Finally, the experimental data on electricity generation are extracted and results similar to the expectations raised in a theoretical analysis are found. These results can be used to identify possible applications.
Keywords Bicycle, end effect, linear generator, suspension.
-
1. Introducción
La generación de energía eléctrica es uno de los temas de principal interés en la sociedad actual. A través de los años se han diseñado diferentes tipos de generadores eléctricos para diferentes escalas, dependiendo la aplicación.
Una problemática a la que se enfrenta la sociedad es la contaminación ambiental, debido a generación eléctrica con combustibles fósiles y su generación de CO2 [1]. Por lo cual las recientes investigaciones están dirigidas a aprovechar cualquier mínima cantidad de energía útil de manera “limpia” (i.e. sin la utilización de combustibles) con tal de evitar emisiones.
En la actualidad existen diseños de generadores eléctricos lineales para aprovechar el movimiento oscilatorio de las olas del mar como una fuente de energía renovable [2].
Se ha encontrado que en estos generadores ocurre un fenómeno llamado “efecto fin” en el cual la forma del voltaje inducido en el embobinado presenta una distorsión causada por cambios de velocidad en los bordes de este [3]. Nuevas investigaciones están enfocadas en el diseño geométrico del generador para evitar este fenómeno.
El objetivo de este artículo es presentar un estudio de la colocación de un generador eléctrico lineal en bicicletas montañeras, las cuales suelen ser utilizados en terrenos irregulares en donde la generación de energía sería más significativa. Además, se busca determinar el voltaje y corriente que se puede generar en función de la velocidad del ciclista y las irregularidades del terreno. Para ello, se diseña un generador eléctrico lineal y un accesorio para acoplarlo a la suspensión, tomando en cuenta que debe ser de fácil instalación y no dificultar el movimiento natural de la suspensión en cuestión. La data obtenida se muestra y compara con el análisis teórico para identificar posibles aplicaciones.
-
2. Marco teórico
Gracias a los experimentos realizados por Michael Faraday [4], hoy conocemos que un campo magnético que varía con el tiempo es capaz de inducir un voltaje en un circuito cerrado, el cual se puede representar mediante la ecuación (1):
ε = −N d<p = −N dB t A = −NA dB(t) (1)
En donde,
ε: voltaje inducido (fuerza electromotriz).
N: número de vueltas en la bobina.
φ: flujo magnético.
d: razón de cambio de flujo magnético.
A: área encerrada por la bobina.
Bt : densidad de flujo magnético.
Esta densidad de flujo magnético t B , depende de las características de la fuente de campo magnético (imanes permanentes para nuestro caso) [5], como podemos ver en la ecuación (2):
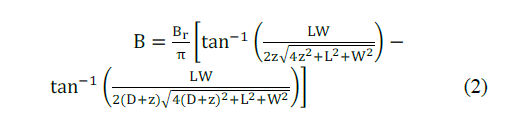
En donde,
Br : campo de remanencia, independiente de la geometría de los imanes.
z: distancia desde una cara polar de los imanes en el eje de simetría variable
L: longitud del imán. W: ancho del imán. D: espesor del imán.
W: ancho del imán.
D: espesor del imán.
La distancia desde una cara polar de los imanes en el eje de simetría variable “z”, se refiere al movimiento de los imanes dentro del circuito cerrado (bobina), el cual depende del tiempo. Esto se aprecia en la figura 1.
-
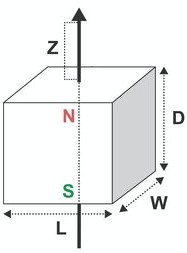
Figura 1. Geometría de la fuente de campo magnético [5].
El movimiento de los imanes dentro de la bobina es exactamente igual al movimiento que describe la suspensión de la bicicleta, ya que ambos se encuentran acoplados. Dicha suspensión está conformada por un resorte y un amortiguador; su movimiento puede ser modelado como una vibración libre con amortiguamiento viscoso [6].
La distancia desde una cara polar de los imanes en el eje de simetría variable “z”, se refiere al movimiento de los imanes dentro del circuito cerrado (bobina), el cual depende del tiempo. Esto se aprecia en la figura 1.
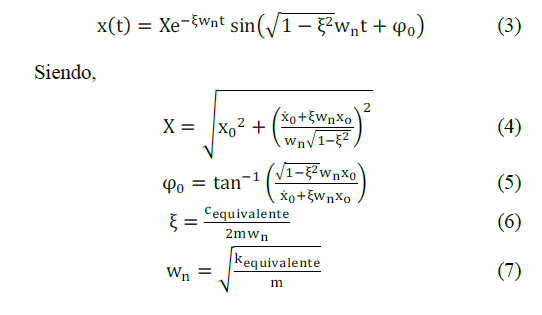
En donde,
x(t): desplazamiento de la suspensión (de los imanes dentro de
la bobina).
0 x : desplazamiento inicial de la suspensión.
0 x& : velocidad inicial de la suspensión.
ξ: factor de amortiguamiento.
m: masa que recae sobre la suspensión (masa ciclista).
equivalente k : constante de rigidez de los resortes en paralelo (configuración de la suspensión delantera de la bicicleta).
c : coeficiente de amortiguación de los amortiguadores
en paralelo (configuración de la suspensión delantera de la
bicicleta).
n ω: frecuencia natural.
La velocidad a la que se mueve la suspensión en una bicicleta puede ser considerada como la componente vertical de la velocidad a la que se mueve dicho vehículo al momento del salto. Esta velocidad puede ser determinada mediante la aplicación de la segunda ley de Newton [8], representada en la
ecuación (8).

- En donde,
ΣF: suma de los pesos de la bicicleta y el ciclista.
m: masa combinada de la bicicleta y el ciclista.
dv (ciclista) : cambio en la velocidad del sistema (bicicleta +
ciclista).
La teoría nos señala que el tiempo de descarga de un
capacitor está determinado por la ecuación (9) [8]:
τ = 5RC (9)
En donde,
R: resistencia equivalente del circuito.
C: capacitancia del capacitor.
-
3. Materiales y métodos
- 3.1 Materiales
A continuación, se presentan los materiales necesarios para la construcción del generador eléctrico lineal, el diseño del acople, así como las especificaciones de la bicicleta utilizada.
-
3.1.1 Características de los imanes permanentes
Se presentan las características importantes de los imanes para el desarrollo del generador.
- Composición: imán de grado N45; compuesto por neodimio, hierro y boro; con un recubrimiento de níquel y cobre [9].
- Campo de remanencia: 13500 Gauss (1.35 T).
- Dimensiones: 3/4” x 3/8” x 1/4” (1.9 mm x 9.5 mm x 6.4 mm).
- Cantidad de imanes utilizados en conjunto: 10 (idénticos).
Además, se necesitó del uso de un transductor de campo magnético (TMAG v.2) para la medición del campo generado por dichos imanes.
-
3.1.2. Características de la bobina
Los parámetros dimensionales de la bobina, luego de su construcción como se aprecia en la figura 2, se presentan como sigue.

Figura 2. Bobina construida para el generador eléctrico lineal.
- 3.1.3. Características de la bicicleta
Para el análisis teórico es necesario conocer ciertos parámetros de la bicicleta como los siguientes.
Máximo recorrido de la suspensión: 10.5 cm.
Constante de resorte individual (k): 6740 N/m. (kequivalente = 13480 N/m).
Constante de amortiguamiento individual (c): 581 Ns/m. (cequivalente = 1162 Ns/m).
Se aclara que la suspensión solo se encuentra en la parte delantera de la bicicleta.
-
3.1.4. Diseño del acople
Con el objetivo de realizar un análisis experimental, siendo la hipótesis la generación de voltaje debido al movimiento de la suspensión de la bicicleta, primero se observa la bicicleta para determinar un punto de instalación que no incomode al usuario y que no afecte las funcionalidades previas del vehículo. Se identificó la ubicación y se tomaron medidas.
Las piezas se diseñaron en el programa Inventor Professional 2017 y se imprimieron en una impresora 3D
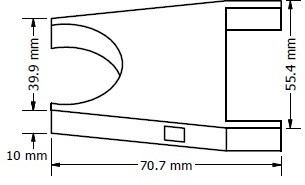
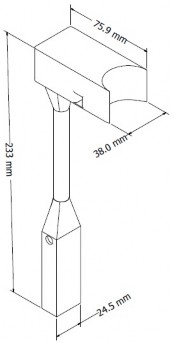
(“MakerBot Replicator 2”, USA). En la figura 3 se muestra el diseño de un soporte superior, soporte inferior para la bobina y un soporte para los imanes con las dimensiones apropiadas para que, al moverse la suspensión, se induzca un voltaje en las terminales del embobinado. Su acople a la bicicleta se muestra en la figura 4.
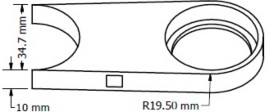
(a)
(b)
(c)
Figura 3. Soporte superior (a) e inferior (b) de la bobina y soporte de los imanes (c).

Figura 4. Acople del sistema a la bicicleta.
-
3.2. Métodos
Se realizó una investigación evaluativa y experimental para identificar la potencia generada con un generador eléctrico lineal. Se evaluó teóricamente el sistema y luego se comparó con los resultados obtenidos experimentalmente.
Para determinar el voltaje inducido de manera teórica, se realizaron los cálculos en el orden mostrado en la figura 5.
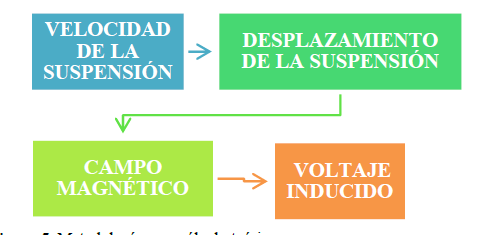
Figura 5. Metodología para cálculo teórico.
Para determinar la longitud de la bobina y del arreglo de imanes permanentes, además de las limitaciones del espacio disponible, se tomó en cuenta que se debe evitar que los imanes salgan de la bobina durante su recorrido normal para evitar el efecto fin ya que, al deformar la onda de voltaje, disminuye la eficiencia del generador [3].
- 3.2.1. Casos de estudio realizados
Para comprobar la funcionalidad del sistema de generación de electricidad mediante el movimiento de una suspensión, se realizaron dos casos de estudio: el primero desde un laboratorio de la Universidad Tecnológica de Panamá y el segundo desde un resalto típico de la Avenida B de dicha universidad (ver
figura 6a), en el cual se iniciaba desde un punto fijo metros arribas del resalto y tratando de mantener iguales condiciones entre una prueba y otra. Se utilizó un ciclista fijo para dichas pruebas (ver figura 6b), cuyo dato de masa se presenta en la tabla 1.
Estos casos de estudio cuentan con un enfoque teórico (o ideal) y otro práctico (o real), de manera que se validaran las fórmulas utilizadas con lo obtenido en las pruebas experimentales.

(a)

(b)
Figura 6. Pruebas de campo en la Universidad Tecnológica de Panamá
(a) y ciclista utilizado para el caso de estudio #2 (b).
Caso de estudio #1: se utilizó un desplazamiento controlado para los imanes dentro de la bobina.
- Análisis teórico: se eligió una expresión para dicho desplazamiento y con ella se obtuvo la expresión de voltaje inducido.
- Análisis práctico: se desplazaron los imanes de manera constante dentro de la bobina y se obtuvo la gráfica de voltaje inducido y la corriente generada.
Caso de estudio #2: se realizaron pruebas con un ciclista en un resalto de una carretera.
-
Análisis teórico: con ciertos datos del terreno, en donde se realizaron las pruebas, se obtuvo la expresión para el desplazamiento de la suspensión y con ella la expresión para el voltaje inducido.
-
Análisis práctico: de dichas pruebas se obtuvo la gráfica del voltaje inducido mediante la utilización de un circuito para obtención de datos. El máximo recorrido de la suspensión se obtuvo utilizando un imán como indicador en la parte inferior. Al moverse la suspensión al pasar por el resalto, el imán recorre esa misma distancia y se mide dicha distancia. Este método se ilustra en la figura 7.

(a)

(b)
Figura 7. Imán indicador en (a) la posición inicial y (b) la posición final.
- 3.2.2 Diseño de circuito para obtención de datos
Para obtener los datos de los casos de estudio se utilizó un microcontrolador (Arduino Uno R3, Arduino) con una placa registradora de datos (Data logger shield, Arduino) conectado a un circuito rectificador (puente de diodos, inductor y capacitor) y un arreglo de resistencias que permite realizar mediciones de hasta 15 V utilizando un divisor de voltaje, anticipado por un capacitor de 4700 , como se aprecia en la figura 8. Para los análisis, se miden los valores de voltaje, tanto en las resistencias, como en el capacitor y se calculan las de corriente.
-
Análisis teórico de la generación
-
Caso de estudio #1: Velocidad controlada en laboratorio
Se eligió un movimiento oscilatorio de forma arbitraría para los imanes descrito por la ecuación (10).
z = 0 005 + 0 005 cos(62 8t) (10)
Que al reemplazarlo junto con las dimensiones de los imanes en la ecuación (2) da como resultado la ecuación (11).
B= 1 35 [tan-1 ( 0 0019*0 0095 )] -
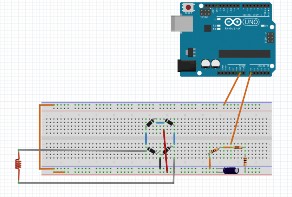
Figura 8. Circuito de voltaje inducido rectificado proveniente de la bobina.
-
4. Discusión y resultados
- 4.1 Estudio sobre los imanes permanentes
Con la finalidad de determinar la cantidad de imanes que maximizaran la generación eléctrica según las dimensiones de nuestra bobina y el espacio con el cual se cuenta en la bicicleta, se procedió a determinar el campo magnético de los imanes utilizados en las pruebas con el transductor de campo magnético. De esta medición se obtuvo, en primera instancia, que a partir de cinco imanes no se presenta gran variación en dicho campo magnético al seguir aumentando la cantidad de imanes.
Por otra parte, en la gráfica 1 se presenta la densidad de flujo magnético en función de la distancia de los imanes a la bobina (ecuación (2)), para distintas cantidades de imanes. En ella se observa que hay una diferencia significativa en la densidad de flujo magnético generado por uno, dos y cinco imanes. Sin embargo, la densidad de flujo magnético generada por diez imanes no difiere de manera considerable a la generada por cinco imanes, por lo que se comprueba lo obtenido en las mediciones y se decide no utilizar una cantidad mayor de imanes, puesto que el costo que representa no sustenta los resultados obtenidos.

Gráfica 1. Densidad de flujo magnético en función de la distancia desde una cara polar de los imanes en el eje de simetría variable (Bt vs z).
-1 0 0019*0 0095 2(0 64+z)J4(0 64+z)2+0 000451 tan ( ) (11)
Partiendo de la ecuación (1) y de las características de la bobina y los imanes descritas en los materiales, obtenemos el voltaje inducido en la gráfica 2, cuya expresión se muestra en la ecuación (12).
dt
E = -2000 * 0 000181 * dB(t) (12)
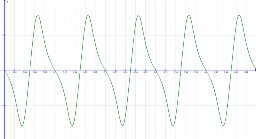
Gráfica 2. Voltaje inducido en la bobina por el movimiento de los imanes ante un desplazamiento descrito por z.
-
Caso de estudio #2: Resalto en una carretera
Se realizaron pruebas y mediciones de un ciclista al pasar por un resalto, para así determinar los datos necesarios de dicho resalto y ciclista presentados en la tabla 1.
|
Característica
|
Valor
|
|
Ángulo de inclinación del resalto (θ)
|
19.13º
|
|
Longitud del resalto
|
0.15 m
|
|
Velocidad inicial del ciclista ( v0 )
|
4.35 m/s
|
|
Masa del ciclista
|
59.87 kg
|
|
Gravedad (g)
|
9.81 m/s²
|
|
Desplazamiento de la suspensión al pasar por el resalto
|
3.1 cm
|
Tabla 1. Datos de la prueba en el resalto de una carretera
Partiendo de la segunda Ley de Newton mostrada en la ecuación (8) y despreciando la resistencia del aire y la fricción con el suelo (por simplificación de los cálculos), se tiene la ecuación (13) y se resuelve para obtener las ecuaciones (14), (15), (16) y (17).
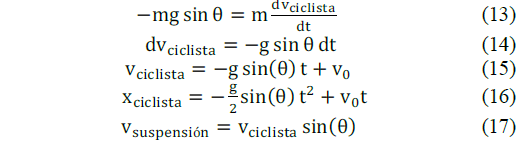
- En donde,
vciclista: velocidad lineal del ciclista durante el resalto.
xciclista: posición del ciclista dentro del resalto.
suspensión 0 v =x& : velocidad inicial de la suspensión.
θ: inclinación del resalto.
vo: velocidad inicial (justo antes de iniciar el resalto).
t: tiempo entre el primer y último contacto de las ruedas de la bicicleta con el resalto.
Utilizando las expresiones de las ecuaciones (13) y (17) y los datos de la tabla 1, obtenemos los valores presentados en la tabla 2.
Tabla 2. Datos obtenidos del análisis de la segunda Ley de Newton
|
Característica
|
Valor
|
|
t en xciclista =0.15m
|
0.035 s
|
|
vciclista
|
4.24 m/s
|
|
vsuspensión =x&0
|
1.39 m/s
|
Para nuestro caso, la masa que recae en las dos partes de la suspensión delantera de la bicicleta es del 40% de la masa total (bicicleta + ciclista) [7], es decir, m= 0.4mtotal
Adicionalmente, al considerar que el desplazamiento de la suspensión al inicio del resalto (perturbación) es cero (x0=0), las características de la suspensión antes descritas (kequivalente y cequivalente) y utilizar las ecuaciones (3) y (7), obtenemos los datos de la tabla 3 y la gráfica 3.
Tabla 3. Datos obtenidos del análisis de vibraciones
|
Característica
|
Valor o representación
|
|
ω n
|
20.94 rad/s
|
|
ξ
|
0.9
|
|
X
|
0.152
|
|
x(t)
|
0.152e-18.46tsen(9.12t)
|
Debido a que x(t) = z, conociendo las dimensiones de los imanes y la expresión de la densidad de campo magnético descrita en la ecuación (2) se obtiene la ecuación (18).

Entonces, partiendo de la ecuación (1) y conociendo las características de los imanes y la bobina se grafica el voltaje inducido se puede apreciar en la gráfica 2 y se obtiene la expresión del voltaje inducido mostrado en la ecuación (19).

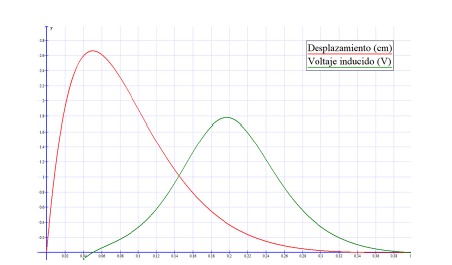
Gráfica 3. Desplazamiento de la suspensión (cm vs t) y voltaje inducido en la
bobina (V vs t) provocado por el paso de la bicicleta sobre el resalto.
Al comparar el máximo desplazamiento de la suspensión obtenido en la gráfica 3 (2.4 cm) con el medido en las pruebas y presentado en la tabla 1 (3.1 cm), se presenta una diferencia de 7 mm.
-
4.4 Análisis práctico de la generación
-
4.5 Caso de estudio #1: Velocidad controlada en laboratorio Para determinar el voltaje inducido, movimos los imanes dentro de la bobina con un recorrido entre ida y vuelta de 6 cm, a una velocidad constante de 0.67 m/s.
Se obtuvo del osciloscopio la gráfica 4 (5 Vca pico) y del amperímetro una corriente en CC (corriente continua) de aproximadamente 6.7 mA, al conectarle un led como carga; es decir, se obtuvo una potencia de 33.5 mW.
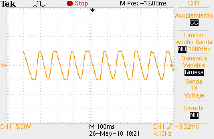
Gráfica 4. Voltaje inducido en la bobina ante el movimiento de los imanes a una velocidad constante, obtenido del osciloscopio.
Al comparar este resultado con el obtenido de manera teórica en el caso de estudio #1, vemos que el voltaje pico es de igual valor (5 Vca), con lo que comprobamos las ecuaciones utilizadas ante una velocidad controlada.
-
4.6 Caso de estudio #2: Resalto en una carretera
La gráfica 5 se obtuvo mediante el circuito descrito en la figura 8, en la misma se observa el voltaje y la corriente inducida en una carga de 30 Ω. El primer pico (de voltaje y corriente) que se obtiene en esta gráfica es producto del movimiento de la suspensión en estudio ante el paso de la llanta delantera de la bicicleta por el resalto, mientras que el segundo pico es producto del paso de la llanta trasera en el cual se da una menor inducción de voltaje y corriente puesto que el movimiento de la suspensión es menor.
Dicho voltaje representa el voltaje rectificado del inducido en la bobina. El voltaje máximo de este valor rectificado es igual al voltaje máximo inducido en la bobina menos la caída de voltaje en los diodos (1.4 V); es decir, el voltaje máximo inducido en la bobina es 2.63 V (1.23 V según la gráfica 5 más 1.4 V por la caída en los diodos).
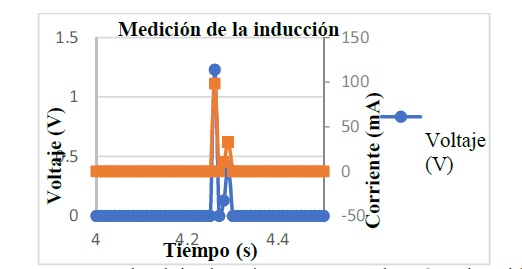
Gráfica 5. Datos de voltaje y la corriente en una carga de 30 Ω, producto del voltaje inducido en la bobina.
Al comparar este resultado con el obtenido de manera teórica en el caso de estudio #2 se observa que el voltaje pico inducido en la bobina difiere por aproximadamente 0.8 V (2.63 V obtenido en la prueba contra 1.8 V obtenido en la gráfica 2). En este caso se cuenta con una potencia de 482.16 mW (debido al pico de corriente de 98.4 mA ante el voltaje de 1.23 V en la carga de 30 Ω), la cual es mayor a la obtenida en el caso de estudio #1. Esto es debido a que la carga conectada tiene la misma impedancia que la bobina; es decir, esta es la potencia máxima que puede ser transferida
En otra ocasión se realizó la prueba de la generación eléctrica midiendo el voltaje en el capacitor de 4700 , de la cual se obtuvo la gráfica 6. En la misma se puede apreciar la ventaja de utilizar el capacitor para el almacenamiento temporal de la energía. Gracias a su tiempo de descarga se hace útil el pico de voltaje generado por el paso de la bicicleta por el resalto; es decir, dicha energía se puede utilizar en un tiempo más prolongado y no disiparse inmediatamente, lo suficiente como para mantener encendido uno o varios ledes.
Si reemplazamos los valores (30 Ω y 4700 ) correspondientes a la resistencia y capacitancia en la ecuación (9), obtenemos un valor de τ = 0.71s. El mismo coincide aproximadamente con la descarga que se puede apreciar en la gráfica 6.
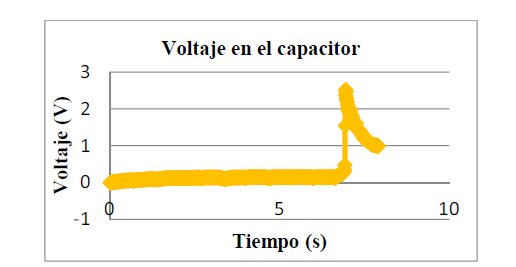
Gráfica 6: Voltaje inducido en la bobina medido desde un capacitor de µF.
Lo ideal sería que se utilice un mejor dispositivo de almacenamiento de energía eléctrica, similar al utilizado para almacenar la energía generada por los paneles solares, el cual soporte la variación de dicha generación (en este caso los picos de voltaje que varían con la irregularidad del terreno por el cual transite el vehículo) y permita utilizar la energía para alimentar equipos más grandes (como celulares, computadoras y baterías de automóviles). Adicionalmente, que sea de un tamaño y peso reducido, para que no incomode a los conductores o afecte la eficiencia del vehículo.
Debido a las exigencias de este dispositivo, nuestro trabajo abarca hasta la utilización de un capacitor.
Cabe señalar que en la gráfica 6 se obtuvo un voltaje relativamente mayor al obtenido en la gráfica 5. Esto pudo deberse a pequeñas alteraciones en la velocidad de la bicicleta y otros factores ambientales, ya que estas pruebas no fueron realizadas en condiciones aisladas dentro de un laboratorio.
5. Conclusiones
Se logró construir, tanto el generador eléctrico lineal como su acople a la bicicleta, de manera satisfactoria para realizar pruebas en la carretera. Fue posible registrar datos de cada prueba con los diseños de circuitos sugeridos.
Al comparar las pruebas realizadas con los cálculos teóricos se observa que en el caso de estudio realizado en laboratorio los resultados son más próximos entre sí. Esto es debido a que en el laboratorio se tiene un mayor control sobre las variables y menos factores que influyan en dichos resultados.
Por otra parte, la diferencia de 7 mm en el desplazamiento de la suspensión entre el análisis teórico y el análisis práctico puede deberse a que la masa resentida en la suspensión sea realmente mayor al 40% de la masa total. Otra razón puede ser que por factores del terreno y el ambiente no considerados, la velocidad del ciclista haya sido mayor a la calculada. Estas variaciones darían un valor mayor en el desplazamiento, según las relaciones de las ecuaciones (3) y (7). Un aumento en el desplazamiento y/o velocidad de la suspensión ocasionaría un mayor voltaje inducido, por lo tanto, estas mismas razones pueden ser la causa de la diferencia de 0.8 V entre el voltaje inducido en la práctica y el calculado.
El sistema propuesto en este trabajo es de fácil instalación. Se puede aplicar a cualquier tipo de vehículo que tenga suspensión o un movimiento similar al de esta, con un cambio apropiado en las dimensiones. Al ser desmontable, permite hacer cambios en las piezas que así lo requieran.
La generación se puede aprovechar aún más con el diseño de una bobina con mayor número de espiras.
La relación entre el análisis teórico y experimental nos da una idea aproximada de lo que podemos generar ante saltos o resaltos en un recorrido en bicicleta de montaña (en el orden de 1 V), siendo resultados satisfactorios.
Para un futuro proyecto, se debe utilizar un circuito que permita almacenar la energía eléctrica en caso de que no se tenga una aplicación para esta al momento de generarla. Además, se recomienda instalar dos bobinas, una en cada lado de la suspensión, para así tener el doble de la energía generada y que la bicicleta se mantenga balanceada.
Los resultados obtenidos en este estudio pueden ser utilizados para identificar posibles aplicaciones para el sistema propuesto.
AGRADECIMIENTOS
La cooperación del profesor Abel Bermúdez (coordinador del departamento de física) por facilitarnos el área de laboratorios para realizar nuestras experiencias.
En nuestras inquietudes técnicas en cuanto a la construcción de nuestro generador acudimos al Dr. Edilberto Hall y al Dr. Dorindo Cárdenas que nos dieron una idea más clara de los fenómenos magnéticos a considerar en el diseño.
Las impresiones 3D de las piezas de nuestro acople fueron gracias a la ayuda de nuestro compañero Octavio Echeverría que nos facilitó su impresora y material.
A nuestro compañero Johan Deruwe por la bicicleta utilizada.
Los imanes de neodimio facilitados por nuestro compañero Jean Carlos Olmos.
El uso del equipo “TMAG v.2” al Dr. Evgeni Cruz.
REFERENCIAS
-
JT, Baker; LH JR, Allen. Effects of CO2 and temperature on rice. Journal of Agricultural Meteorology, 1993, vol. 48, no 5, p. 575-582.
-
Kim, M. Koo, J. Jeong, K. Hong, I. Cho and J. Choi, “Design and analysis of tubular permanent magnet linear generator for small- scale wave energy converter”, AIP Advances, vol. 7, no.5, p. 056630, 2017.
-
A. T. Hernández, M. P. Silva, N. M. Escamilla and L. H. González, “Impacto de la Geometría en el Efecto Fin de Generadores Lineales”, Información tecnológica, vol. 27, no. 4, pp. 133-138, 2016.
-
M. N. Sadiku, Elementos de electromagnetismo. 3ra Edición. México: Oxford, Mar. 2011.
-
Formula for block magnet flux density, Supermagnete, Gottmadingen, Germany.
-
S. S. Rao, Vibraciones Mecánicas, 5ta Edición, México: Pearson, 2012.
-
D. E. Fernández, “Modelado y simulación dinámica de bicicletas de montaña”, Trabajo Fin de carrera, Universidad de Almería, Almería, España, 2012.
-
F. W. Sears and M. W. Zemansky, Física Universitaria: Volumen
-
13va Edición. México: Pearson, 2013.
- eodymium Iron Boron Magnets, Eclipse Magnetics Ltd., Sheffield, England.
